1  Úvod

1.1 Štatistické modelovanie

  • Štatistické modelovanie je rozsiahla sada metód a nástrojov určená na porozumenie dátam.
  • S rozvojom strojového učenia sa zaužíval aj názov štatistické učenie.
  • Sú dva základné spôsoby učenia: asistované a neasistované .
  • Asistované predstavuje výstavbu štatistického modelu na odhad výstupu pomocou jedného či viacerých vstupov.
  • V neasistovanom učení sú vstupy, no žiaden asistujúci výstup. Stále však možno skúmať vzťahy v dátach a ich štruktúru.
Príklad (mzda)
  • Majme súbor údajov o mzde (skupiny mužov v štátoch východného pobrežia USA).
  • Chceme porozumieť súvislosti medzi výškou mzdy zamestnanca a jeho vekom či dosiahnutým vzdelaním, prípadne jej vývoju v čase.

  • Každý zo vstupov môže byť (s väčšou či menšou dávkou neistoty) použitý na predikciu mzdy.
  • Prirodzene, najpresnejšia predpoveď bude s použitím všetkých troch vstupov.
  • Najbežnejšie sú lineárne regresné modely, nie vždy však svojou presnosťou postačujú.
Príklad (reklama)
  • Klient nás ako štatistických konzultantov najal na vyšetrenie súvislosti medzi reklamou a odbytom konkrétneho produktu.
  • Súbor obsahuje údaje o odbyte (sales, v tisícoch jednotiek) a rozpočet na reklamu (v tisícoch dolárov) v troch rôznych typoch médií: TV, rádio, noviny.
  • Ak dokážeme nájsť významnú súvislosť, môžeme klientovi poradiť, v ktorom médiu má posilniť reklamu, aby zvýšil odbyt.
  • Cieľom je teda vyvinúť presný model na predikciu odbytu.

1.1.1 Náhodné premenné a ich vzťah

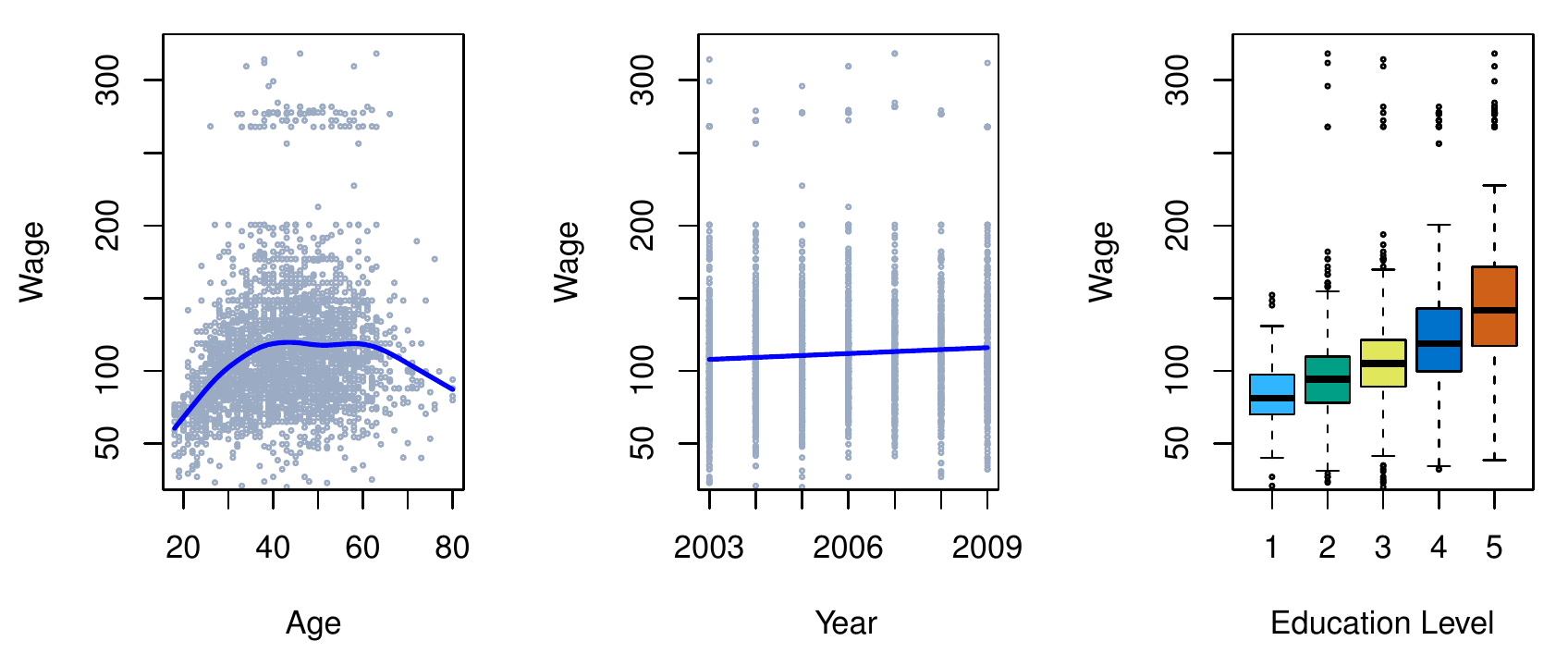
  • Odbyt v predošlom príklade je výstupná premenná – inými slovami odozva (response), závislá premenná.
  • Rozpočet na reklamu (v jednotlivých zložkách) je vstupná premenná – alebo aj prediktor, nezávislá premenná, črta (feature).
  • Vo všeobecnosti, predpokladajme kvantitatívnu odozvu YY a sadu pp rôznych prediktorov, X⃗=(X1,X2,...Xp)\vec X = (X_1,X_2,... X_p). Medzi nimi je nejaký (systematický) vzťah a ten je reprezentovaný (neznámou) funkciou ff, takže Y=f(X⃗)+ε Y = f(\vec X) + \varepsilon kde ε\varepsilon predstavuje náhodnú chybovú zložku, ktorá nezávisí od X⃗\vec X a zvyčajne má nulovú strednú hodnotu.
Príklad (príjem)
  • Predpokladajme, že príjem po skončení školy by sa dal predpovedať pomocou počtu rokov venovaných vzdelaniu.
  • Modrá krivka predstavuje skutočnú funkciu ff. Tú však v praxi nepoznáme, ale za predpokladu určitých vlastností chybovej zložky môžeme ff do istej miery odhadnúť.

1.1.2 Ciele modelovania

  • Prečo vlastne potrebujeme odhad ff?
  • Sú dva hlavné dôvody (ciele modelovania):
    • predpovedanie (prediction) a
    • dedukcia (inference).

1.1.2.1 Predpoveď

  • V mnohých situáciách sú vstupné hodnoty ľahko dostupné, no výstupné sa získavajú ťažko. Pretože chybová zložka sa nasčíta na nulu, predpoveď je jednoduchá: Y^=f^(X⃗) \hat Y = \hat f(\vec X)

  • Tu odhad f^\hat f môže byť (a v strojovom učení často býva) ako čierna skrinka.

  • Význam predikcie je napr. v určení rizika nepriaznivej reakcie na určitý liek ak prediktormi sú charakteristiky pacientovej krvi (získateľné laboratórne). Je lepšie vopred predpovedať reakciu organizmu a tak sa vyhnúť podaniu lieku s nežiadúcim účinkom pri pacientoch s vysokou hodnotou odozvy.

  • Presnosť predpovede závisí na dvoch chybách:

    • redukovateľnej (chyba odhadu funkcie) a
    • neredukovateľnej (šum, vplyv nemeraných premenných, nemerateľnej premenlivosti - reakcia pacienta na liek podľa nálady, odchýľka v zložení tablety atď.) E[(Y−Y^)2]=E[(f(X⃗)+ε−f^(X⃗))2]=(f(X⃗)−f^(X⃗))2+var(ε) \begin{split} E[(Y-\hat Y)^2] & = E\left[\Big(f(\vec X) + \varepsilon - \hat f(\vec X)\Big)^2\right] \\ & = \Big(f(\vec X)-\hat f(\vec X)\Big)^2 + var(\varepsilon) \end{split}

1.1.2.2 Dedukcia

  • Často nás zaujíma spôsob, ako je odozva ovplyvňovaná zmenou vstupov. Preto síce chceme odhadnúť funkciu ff, ale nie kvôli predpovediam, ale analýze jej tvaru.
  • Tu už sa s funkciou nemôže zaobchádzať ako s čiernou skrinkou.
  • Chceme odpovede na otázky
    • Ktoré premenné sú asociované s odozvou?
    • Aký je vzťah medzi YY a jednotlivými prediktormi (kladný, záporný)? Ovplyvňuje ho nejaký iný prediktor?
    • Môže byť tento vzťah zhrnutý do lineárnej rovnice?

1.1.2.3 Ilustrácie cieľov

  • Príkladom modelovania kvôli predikcii môže byť záujem komerčnej spoločnosti identifikovať jedincov ako potenciálnych zákazníkov na základe demografických ukazovateľov, pričom odozva na marketingovú kampaň (pozitívna alebo negatívna) slúži ako výstup. Firmu teda nezaujímajú detaily vzťahu medzi prediktormi a odozvou ale predpovede.
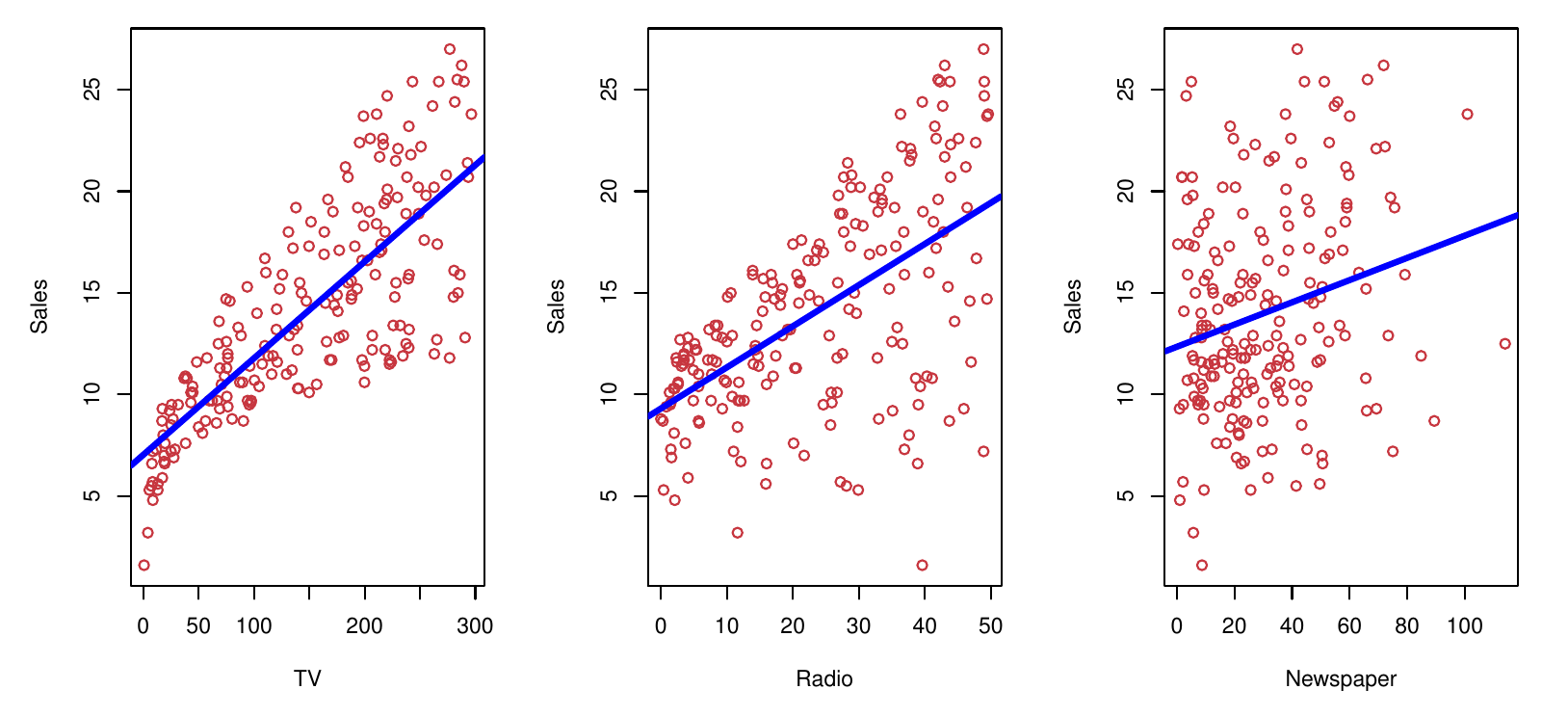
  • V príklade s inzerciou a odbytom naopak môže byť záujem o odpovede na otázky:
    • Ktoré médiá prispievajú k odbytu?
    • Ktoré médiá vytvárajú najväčšie oživenie obchodu?
    • Aké navýšenie predaja možno očakávať s konkrétnou investíciou do reklamy v TV?

1.1.3 Metódy aproximácie skutočnej funkcie

  • Od účelu závisí voľba metódy:

    • jednoduchší ale interpretovateľný model, alebo
    • predikčne výkonný no menej zrozumiteľný model, s ktorým je dedukcia ťažšia.

  • Preberieme viacero lineárnych i nelineárnych prístupov ku odhadu ff. Tieto metódy majú niektoré črty spoločné (a na tie sa zameriame).

  • Majme nn pozorovaní, ktoré sa súhrnne nazývajú trénovacia vzorka, pretože pomocou nich naučíme konkrétnu metódu odhadnuť ff.

  • Nech xijx_{ij} je ii-te pozorovanie jj-teho prediktoru, yiy_i zodpovedajúce ii-te pozorovanie odozvy, pričom i=1,...ni=1,...n a j=1,...pj=1,...p. Potom trénovaciu vzorku tvoria dvojice {(x1,y1),…,(xn,yn)}\{(x_1,y_1),\ldots,(x_n,y_n)\} kde xi=(xi1,xi2,…,xip)x_i=(x_{i1},x_{i2},\ldots,x_{ip}).

  • Cieľom je aplikovať štatistickú metódu učenia na trénovaciu vzorku na odhad neznámej funkcie ff.

  • Väčšina štatistických metód modelovania je charakterizovaných buď ako parametrické, alebo neparametrické.

1.1.3.1 Parametrické metódy

  • Parametrický prístup sa skladá z dvoch krokov

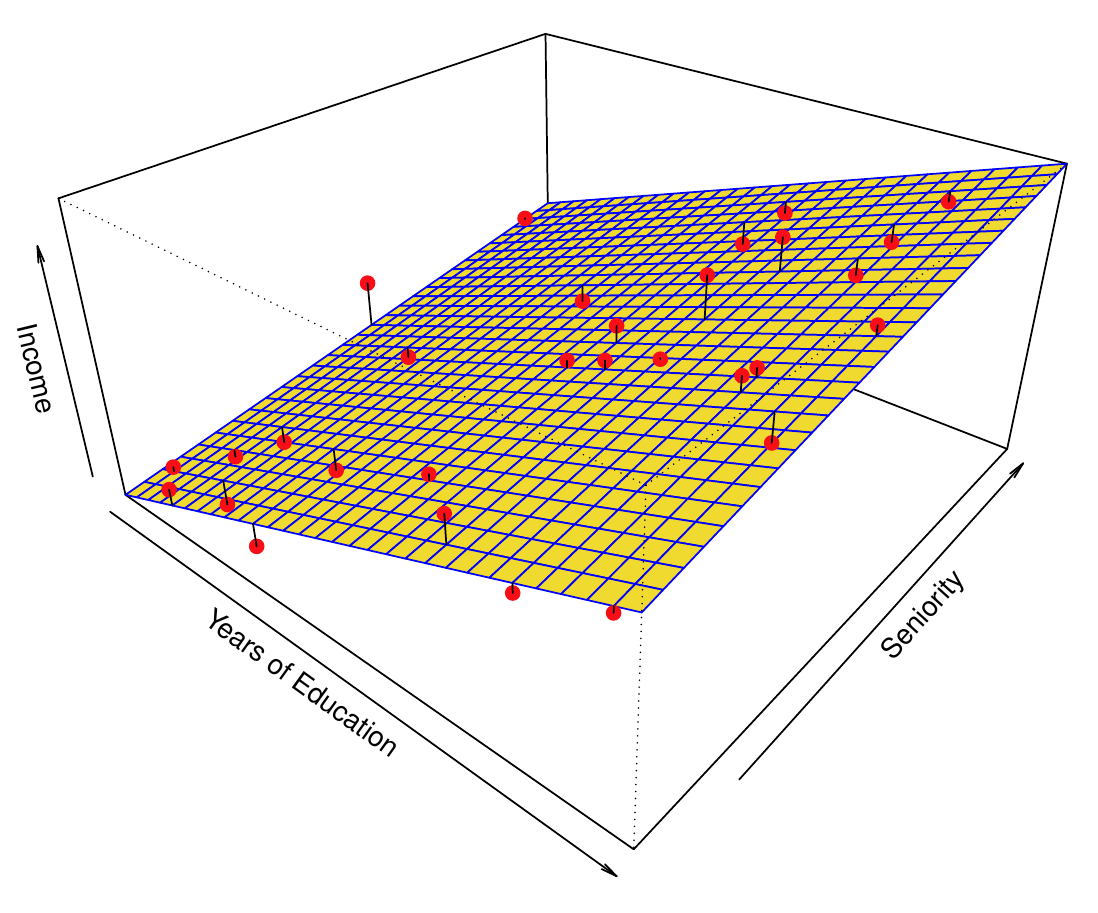
    1. Vytvorenie predpokladu o tvare funkcie (funkčnom predpise), napr. že ff je lineárna v premenných X⃗\vec X, teda f(X⃗)=β0+β1X1+...+βpXpf(\vec X) = \beta_0 + \beta_1 X_1 + ... + \beta_p X_p. Tak sa problém odhadu ff značne zjednodušil (z odhadu celej pp-rozmernej funkcie) na odhad p+1p+1 parametrov β0,...,βp\beta_0,...,\beta_p.
    2. Voľba a použitie metódy, ktorá náš model natrénuje na dátach (napasuje na pozorovania). V prípade lineárneho modelu je to najčastejšie (bežná) metóda najmenších štvorcov.

  • Ukážeme si rôzne funkčné predpisy i metódy odhadu parametrov.

  • Výhoda parametrického prístupu je teda v zjednodušení odhadu.

  • Naopak, jeho potenciálna nevýhoda je v tom, že zvolený model zvyčajne celkom nevystihne skutočný tvar neznámej funkcie ff. To sa síce dá obísť voľbou flexibilnejších modelov, ktoré sú schopné imitovať veľa rôznych tvarov funkcií, no vo všeobecnosti aj vyžadujú odhad väčšieho počtu parametrov.

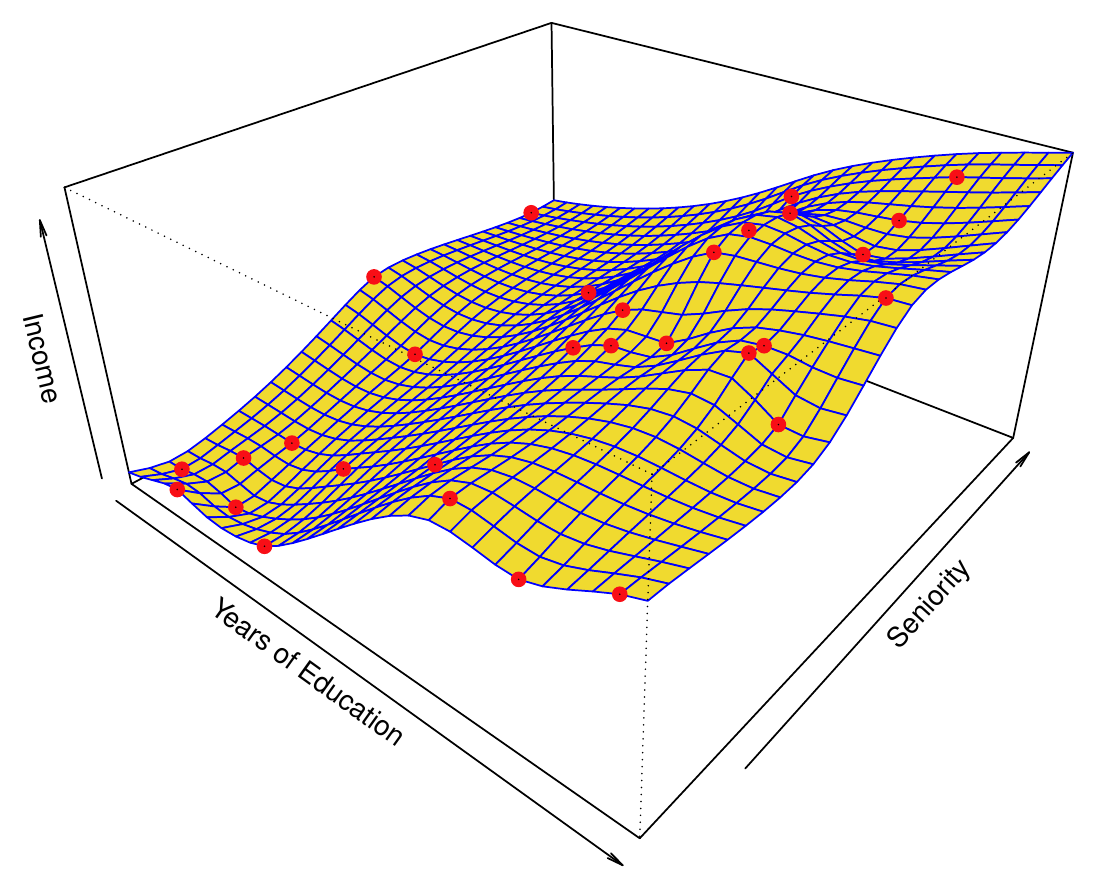
  • A komplexnejšie modely zas môžu viesť k javu, ktorý sa nazýva “overfitting”. Čiže flexibilné modely sú náchylné na prehnanú snahu popísať okrem funkcie aj náhodný šum.

Príklad (príjem)
  • Parametrické metódy si ilustrujeme na príklade závislosti príjmu od vzdelania a skúsenosti (prax, trvanie kariéry) popísanou lineárnym modelom prıˊjem≈β0+β1×vzdelanie+β2×skuˊsenostˇ príjem \approx \beta_0 + \beta_1\times vzdelanie + \beta_2 \times skúsenosť
  • Na obrázku vľavo je skutočný funkčný vzťah (poznáme ho, pretože dáta sú simulované), vpravo jeho lineárna aproximácia.

1.1.3.2 Neparametrické metódy

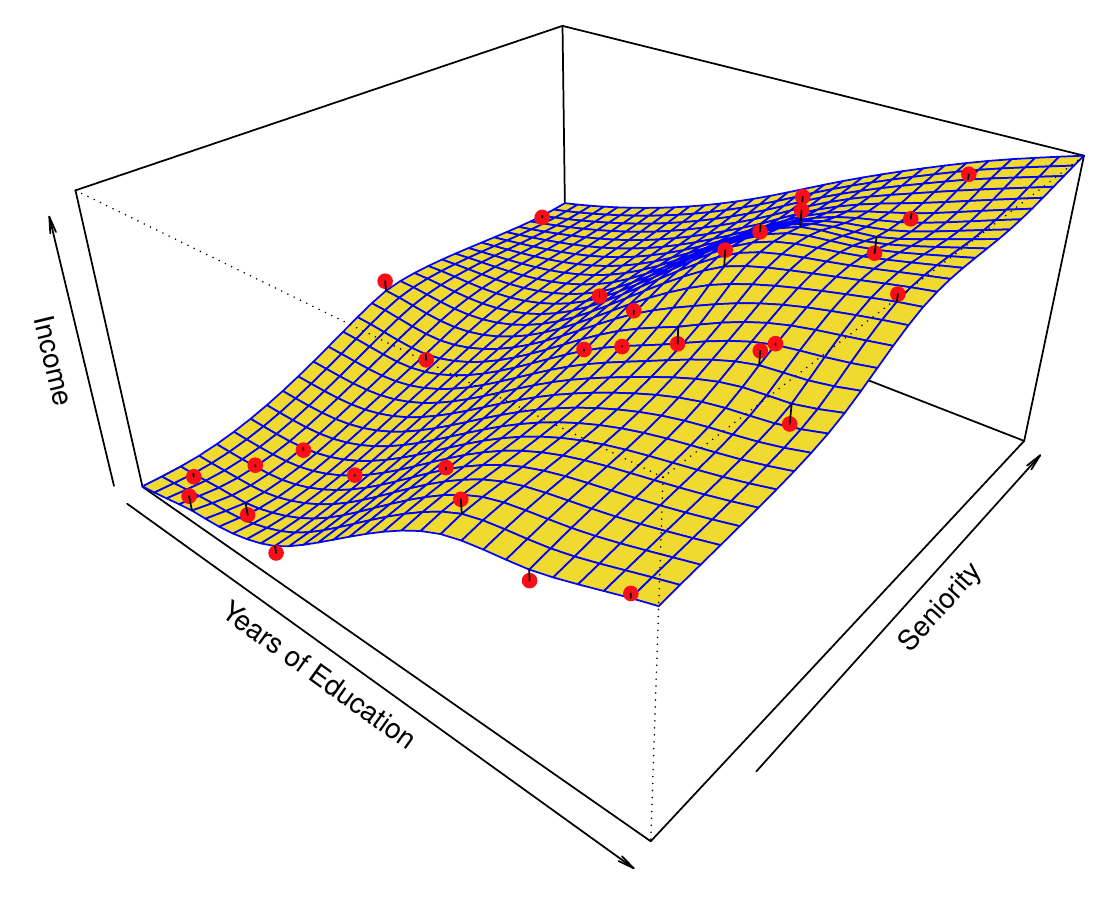
  • Tento prístup sa neobmedzuje na predpoklad o tvare funkcie, ale snaží sa k dátam primknúť čo najtesnejšie bez toho, aby aproximácia bola príliš rovná, alebo naopak, príliš pokrútená.
  • Pretože však neredukuje problém odhadu ff na odhad malého počtu parametrov, jeho hlavnou nevýhodou je nutnosť veľkého počtu údajov.
Príklad (príjem)
  • Nadviažeme na predošlý príklad s príjmom. Na obrázku vľavo je zobrazený neparametrický model zo skupiny vyhladzujúcich splajnov (2D smoothing spline, konkrétne thin-plate spline) s optimálnym stupňom vyhladenia.
  • Na pravom obrázku je splajn s vysokým stupňom aproximácie (nízkym stupňom vyhladenia), ktorý prechádza cez každý bod trénovacej vzorky (prakticky je to interpolačný splajn) a necháva chybovú zložku úplne nulovú.
  • Pravý obrázok je príkladom overfitting-u.

  • Prefitovanie je nežiadúce, pretože znižuje presnosť predpovedí (mimo trénovacej vzorky). Preto potrebujeme metódy na voľbu správneho stupňa vyhladenia.

1.1.3.3 Kompromis (presnosť vs. interpretovateľnosť)

  • S rozvojom IT je nedostatok dát či výpočtová kapacita čoraz zriedkavejším problémom. Prečo by sme potom nemali zakaždým uprednostniť flexibilnú metódu odhadu ff pred tou reštriktívnou?
  • Dôvodom je schopnosť interpretácie modelu, ktorá je žiadúca, ak nám primárne nejde o predikcie ale o dedukciu (porozumenie procesu, ktorý generoval údaje).

1.1.4 Prítomnosť odozvy

  • Väčšina úloh štatistického modelovania spadá do dvoch kategórií – asistované a neasistované – podľa toho, či niektorá z náhodných premenných vystupuje v role vysvetľovanej premennej alebo nie.

1.1.4.1 Asistované učenie

  • Všetky doteraz uvádzané príklady sú z oblasti asistovaného učenia, kde každé pozorovanie hodnôt prediktorov je spojené s pozorovaním odozvy a našim cieľom je modelovať ich vzťah (či už na jeho lepšie pochopenie alebo predpovedanie ďalších hodnôt). Prirodzene sem patria klasické metódy ako lineárna či logistická regresia, ale i množstvo novších (GAM, boosting, SVM, ANN).

1.1.4.2 Neasistované učenie

  • Na druhej strane, neasistované učenie je náročnejšie v tom, že žiadne pozorovanie odozvy k dispozícii nie je. Akoby sme modelovali naslepo. Typickým príkladom je zhluková analýza (clustering), v ktorej sa na základe podobných hodnôt premenných pozorovania zatrieďujú do relatívne odlišných skupín. Napr. pomocou takých charakteristík, ako sú PSČ, príjem v rodine a nákupné návyky, chceme pozorovania (zákazníkov) zatriediť do skupín s veľkými výdavkami na nákupy (tí, čo veľa míňajú) a s nízkymi výdavkami (sporovliví).

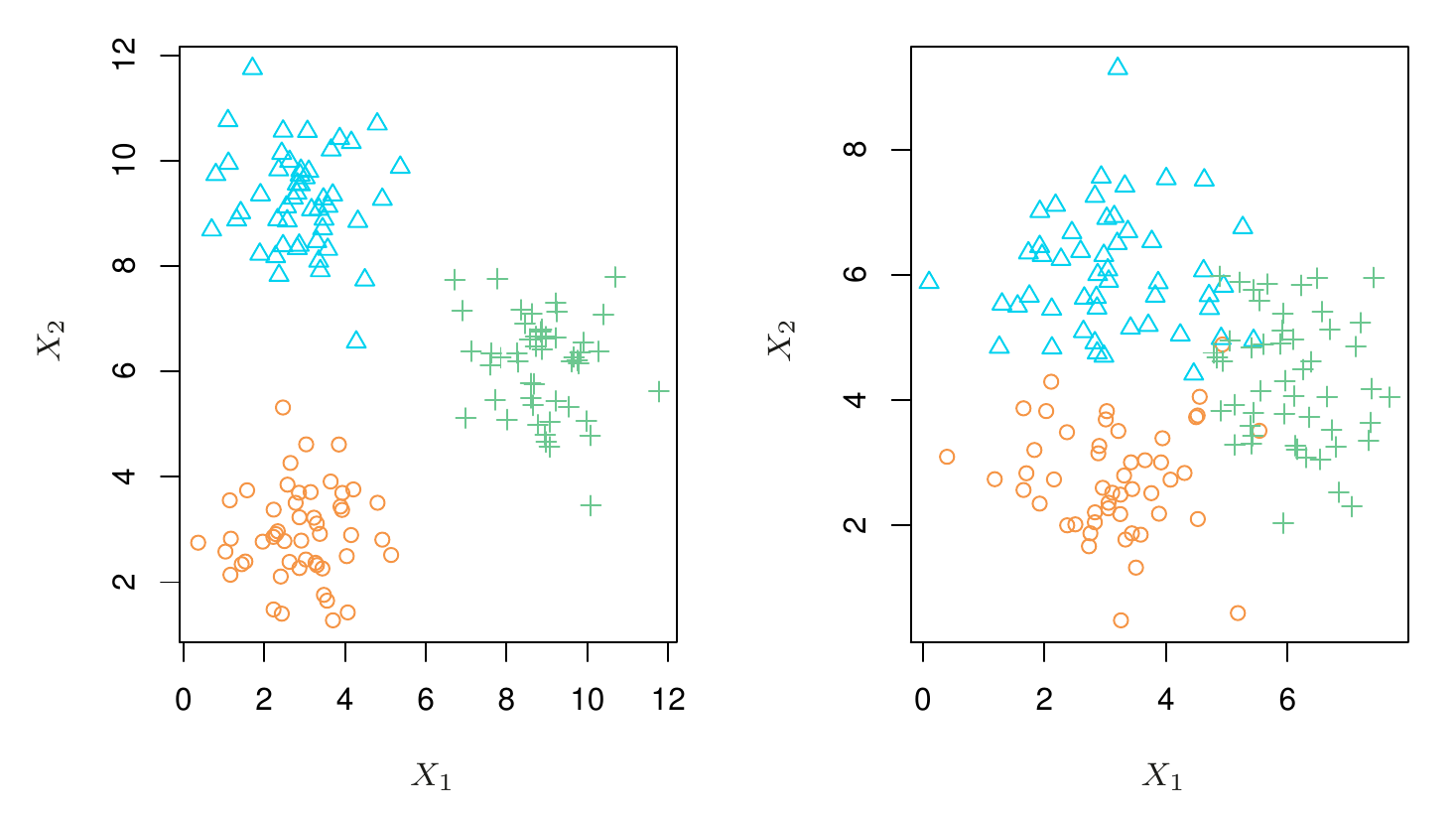
  • Na ilustračnom obrázku vľavo sú skupiny jasne odlíšené (takže zhlukovanie je jednoduché) zatiaľčo vpravo sú značné presahy medzi skupinami (zhlukovanie je veľmi obtiažne).
  • Ak je prediktorov viac, pp, jeden bodový graf nestačí, treba ich p(p−1)/2p(p-1)/2, a tak namiesto vizuálneho posúdenia sa musíme spoľahnúť na automatické metódy.
  • V jednej úlohe je možné aj kombinovať oba prístupy, napr. keď hodnoty odozvy sú dostupné iba pre časť pozorovaní prediktorov: polo-asistované učenie (semi-supervised).

1.1.5 Typ odozvy (regresia vs. klasifikácia)

  • Premenné sa delia na kvantitatívne a kvalitatívne (kategorické), resp. spojité a diskrétne
  • Napr. {vek, výška, príjem, cena} oproti {stav, pohlavie, značka, indikácia zadĺženia, druh choroby}
  • Modelovanie
    • kvantitatívnej odozvy sa označuje ako regresná úloha (napr. lineárna regresia MNŠ)
    • kvalitatívnej odozvy ako klasifikačná úloha
  • Hranica medzi nimi nie je vždy ostrá, napr. pre binárne premenné sa používa logistická regresia, ktorá napriek svojmu názvu je klasifikačnou metódou, ale keďže priamo modeluje pravdepodobnosť zaradenia do jednotlivých tried, má veľa spoločné s lineárnou regresiou.
  • Niektoré metódy ako k-najbližších susedov sa dajú použiť v oboch kontextoch (úlohách).
  • Typ premenných v úlohe prediktorov je menej podstatný, pred samotnou analýzou sa však predpokladá ich správne “kódovanie”.

1.2 Vyhodnotenie modelu

  • Cieľom predmetu je zoznámiť sa so širokou paletou nástrojov štatistického modelovania.
  • Prečo?
  • Pretože neexistuje niečo ako supermetóda, ktorá funguje najlepšie v každej situácii, pre každý dataset.
  • Výber najvhodnejšej metódy je tak dôležitou úlohou štatistického modelovania a prakticky môže byť jednou z jej najnáročnejších častí.

1.2.1 Meranie kvality

  • Na výber vhodnej metódy budeme potrebovať nejakú mieru zhody modelu s realitou, predikcie s pozorovaním.

  • V regresnej úlohe je najčastejšie používanou mierou stredná kvadratická chyba (mean squared error) MSE MSE=1n∑i=1n(yi−f^(xi))2 MSE = \frac1n \sum_{i=1}^n\Big(y_i - \hat f(x_i)\Big)^2 ktorá je malá, ak všetky predpovede sú blízko skutočnej odozvy, a veľká, ak sa niektoré odhady od reality značne odlišujú.

  • Ak sa MSE vypočíta z rovnakých údajov, ako na ktorých bol model natrénovaný, mala by sa označiť pojmom trénovacia MSE.

  • Zvyčajne nám však neveľmi záleží na tom, ako model funguje na známych dátach, ale naopak, chceme poznať presnosť predpovedí, keď (už natrénovaný) model aplikujeme na nové dáta.

Prečo?
  • Predpokladajme, že chceme zbohatnúť na obchodovaní s akciami. Vytvoríme model, ktorý pomocou predošlých výnosov odhadne aktuálnu cenu. Teraz už len spoľahlivo zistiť, či bude cena zajtra rásť (a treba nakupovať), alebo klesať (a akcie rýchlo predať).
  • Alebo majme klinické záznamy (napr. hmotnosť, tlak, výška, vek, rodinná anamnéza) určitého počtu pacientov, o ktorých vieme aj to, či majú cukrovku alebo nie. Tieto záznamy použijeme na natrénovanie modelu. Predpovede z neho však nepotrebujeme na overenie, či pacient z našej skupiny cukrovku má (pretože to vieme), ale na predikciu rizika pri budúcich pacientov (na základe ich klinických záznamov).
  • Formálne, ak trénovacia vzorka je (x1,y1),...,(xn,yn)(x_1,y_1),...,(x_n,y_n), označme nové pozorovanie ako (x0,y0)(x_0,y_0). Zaujíma nás, ako vybrať štatistickú metódu, ktorá minimalizuje nie trénovaciu MSE ale E[(y0−f^(x0))2]E[(y_0-\hat f(x_0))^2], čiže tzv. testovaciu MSE.
  • Na to je potrebná testovacia vzorka.
  • Trénovacia MSE nie je dobrou náhradou testovacej MSE.
Ilustrácia (nelinárna funkcia)

  • Na ľavom obrázku je skutočná funkcia závislosti Y od X (čierna), dáta z nej simulované (body), lineárny regresný model (oranžová priamka) a dve splajnové krivky (modrá a zelená).
  • Napravo je graf trénovacej MSE (sivá), testovacej MSE (červená) a najmenšej dosiahnuteľnej testovacej MSE (prerušovaná), ktorá sa rovná neredukovateľnej chybe predpovedí, var(ε)var(\varepsilon). Prvé dve sa menia s prispôsobivosťou modelov, ktorá sa formálne označuje ako stupne voľnosti modelu. Najmenej stupňov voľnosti tu má priamka (oranžové štvorce), ktorá - ako vidno aj z testovacej MSE - nedostatočne aproximuje skutočnú funkciu. Modrá splajnová krivka je blízko optimálnej. Zelený model je reprezentovaný bodom na vzostupnej časti grafu testovacej MSE, pretože sa príliš vlní (overfitting).
  • To, že trénovacia chyba je (takmer) vždy menšia ako testovacia je dané tým, že väčšina štatistických metód odhadu (priamo alebo nepriamo) minimalizuje trénovaciu MSE.
Ilustrácia (takmer lineárna funkcia)

  • V tomto prípade lineárny model je blízky optimálnemu, preto prevážia jeho interpretačné vlastnosti a býva uprednostnený pred lepším, ale zložitejším modelom.
  • V praxi sa testovacia chyba odhaduje z trénovacích dát pomocou resamplovacích metód, konkrétne tzv. krížovou validáciou.

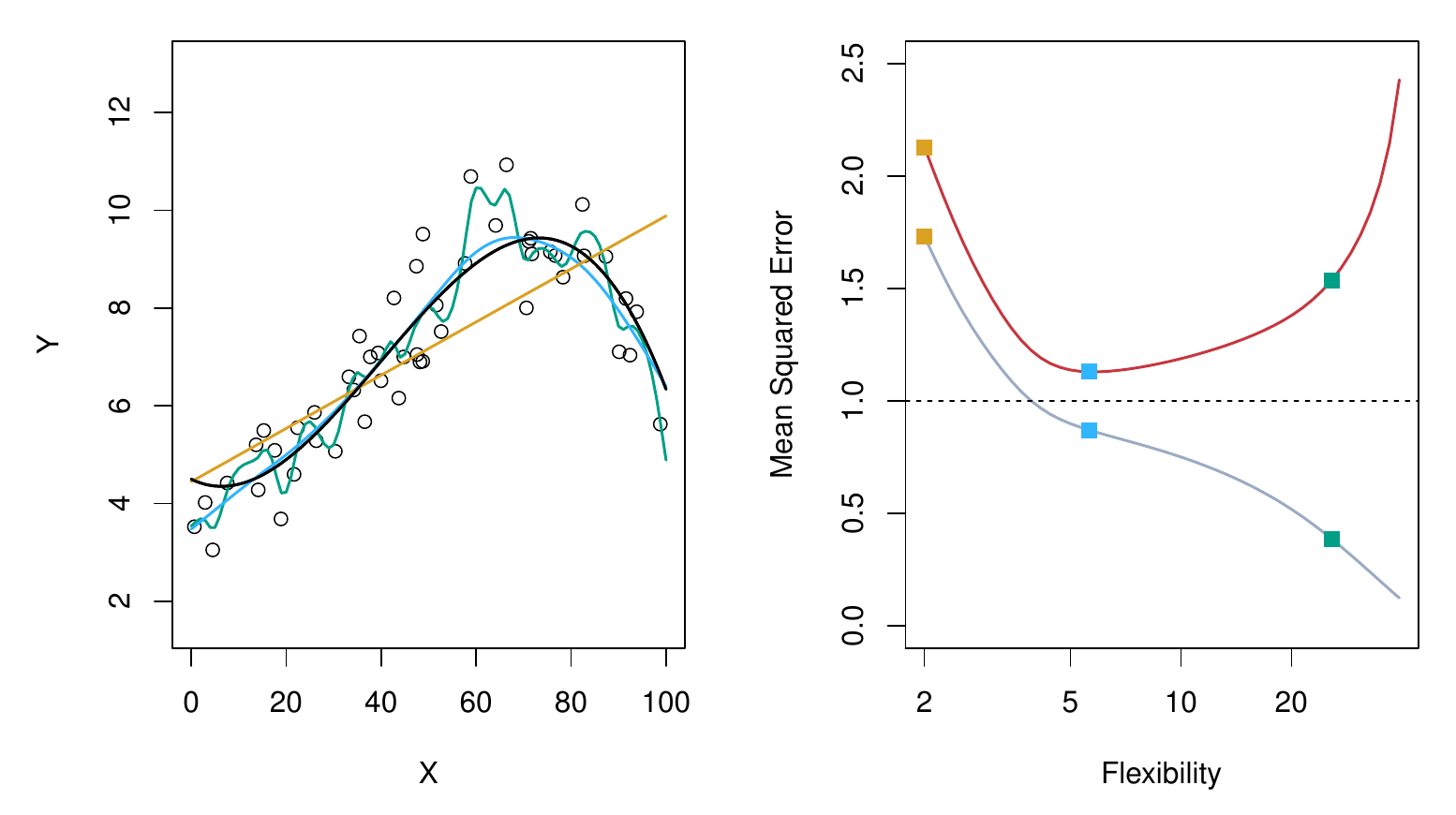
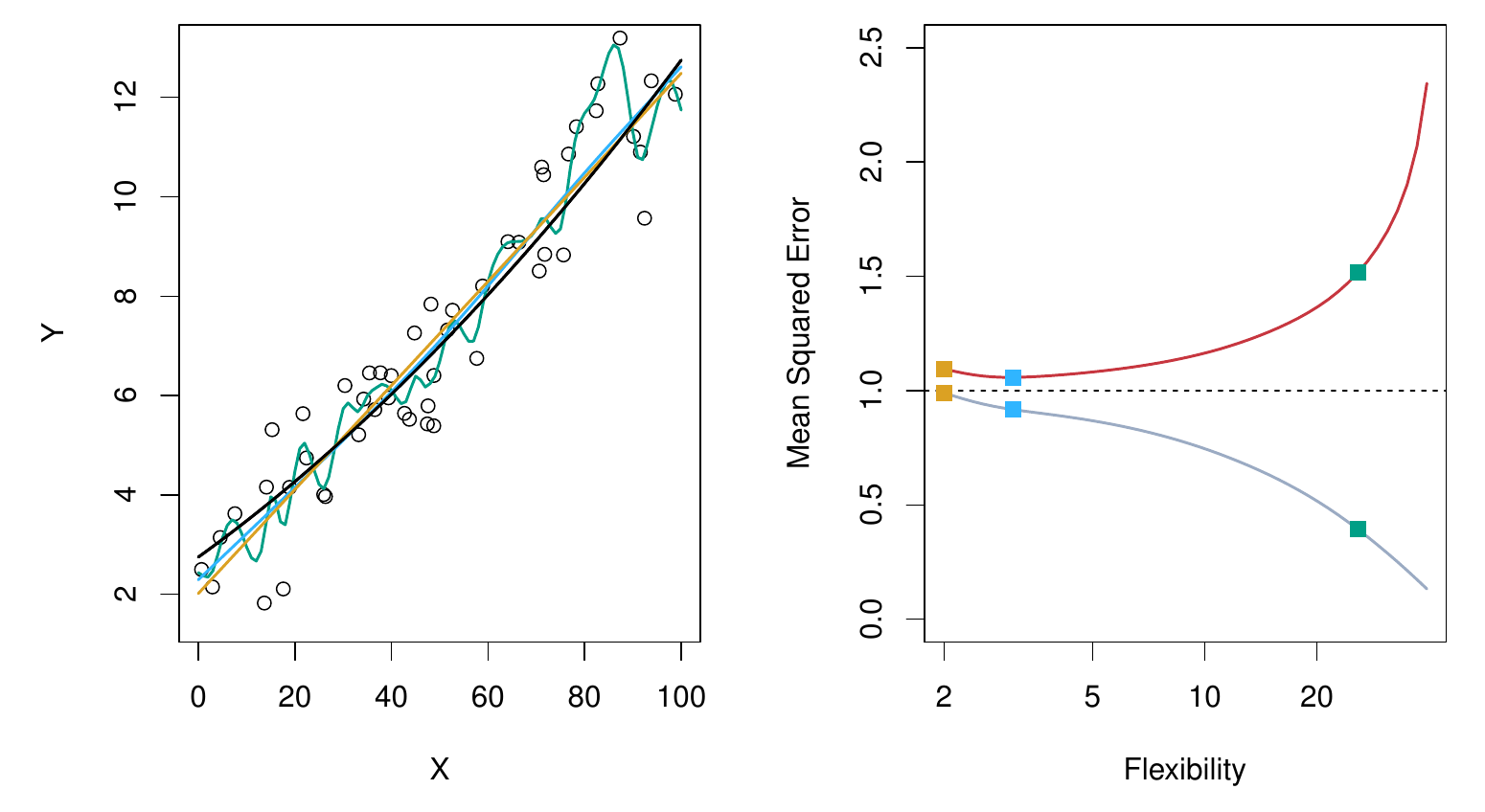
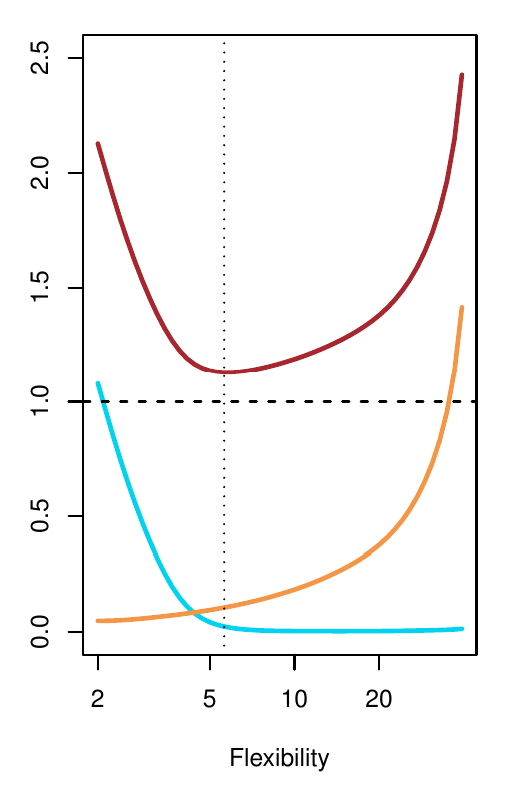
1.2.2 Kompromis (výchyľka vs. rozptyl)

  • Tvar písmena U grafu testovacej MSE je dôsledkom kompozície dvoch druhov chýb: variancie predpovede f^(x0)\hat f(x_0) a vychýlenia (bias) predpovede.
  • Celkovo teda môžeme testovaciu MSE rozložiť ako vo vzťahu E[(y0−f^(x0))2]=var(f^(x0))+[bias(f^(x0))]2+var(ε) E\left[(y_0-\hat f(x_0))^2\right] = var(\hat f(x_0)) + [bias(\hat f(x_0))]^2 + var(\varepsilon)
  • Optimálny model tak získame minimalizáciou rozptylu a súčasne aj výchylky.
  • Variancia predstavuje mieru, do akej by sa odhad funkcie zmenil, ak by sme na trénovanie modelu použili iný náhodný výber (z rovnakej populácie). To znamená, že ohybnejšie modely sú citlivejšie na zmeny v dátach.
  • Bias predstavuje chybu aproximácie (zložitej) skutočnosti (jednoduchým) modelom.
  • Nájsť dobrý kompromis medzi oboma chybami (bias-variance trade-off) je jednou z hlavných tém štatistického modelovania.

1.2.3 Presnosť v klasifikácii

  • Všetky spomenuté princípy platia aj pri klasifikačnej úlohe, iba namiesto strednej kvadratickej chyby použijeme mieru vhodnú pre kvalitatívnu premennú, napr. chybovosť (error rate, ER). Trénovacia ER sa vypočíta vzťahom ER=1n∑i=1nI(yi≠y^i) ER = \frac1n \sum_{i=1}^n I(y_i \neq \hat y_i) kde I(x)I(x) je indikačná funkcia, ktorá sa rovná 1 ak podmienka xx je splnená, inak sa rovná 0.
  • Testovacia ER je definovaná analogicky ako MSE, čiže ako stredná hodnota ER pre nové pozorovanie, E[I(y0≠y^0)]E\left[I(y_0 \neq \hat y_0)\right].
  • Dobrý klasifikátor je taký model, pre ktorý je testovacia ER najmenšia.
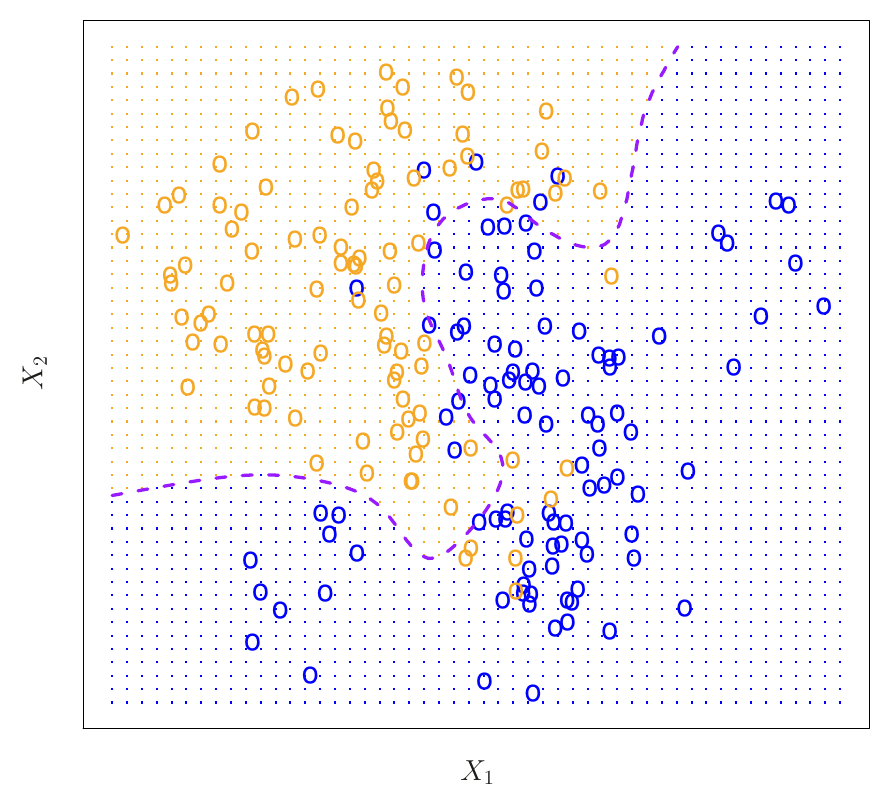
  • Dá sa ukázať, že takúto vlastnosť spĺňa jeden jednoduchý klasifikátor, ktorý každé pozorovanie zaradí do najpravdepodobnejšej triedy (podmienenej hodnotami prediktorov), teda do triedy jj pre ktorú podmienená pravdepodobnosť Pr(Y=j∣X⃗=x⃗0) Pr(Y=j|\vec X=\vec x_0) je najväčšia. Takýto klasifikátor sa nazýva Bayesov.
  • V prípade binárnej odozvy je tou hraničnou pravdepodobnosťou hodnota 1/2. V priestore prediktorov tvorí tzv. Bayesovu rozhodovaciu hranicu.
Ilustrácia (Bayesova rozhodovacia hranica)