lm(wage ~ cut(age, 4), ISLR2::Wage) |>
summary() |>
coef() |>
signif(2) Estimate Std. Error t value Pr(>|t|)
(Intercept) 94.0 1.5 64.0 0.0e+00
cut(age, 4)(33.5,49] 24.0 1.8 13.0 2.0e-38
cut(age, 4)(49,64.5] 24.0 2.1 11.0 1.0e-29
cut(age, 4)(64.5,80.1] 7.6 5.0 1.5 1.3e-01dat <- ISLR2::Wage # |> dplyr::slice_sample(n = 100)
grid <- modelr::seq_range(dat$age, 100) |>
data.frame(age = _)
# --- discontinuous ---
# function to discretize continuous variable by breaking into bins
# in: x - numeric vector to be discretized
# knots - numeric vector of breaks (without extremes)
# - single integer, number of breaks
# out: character vector indicating intervals
make_ind <- function(x, knots) {
min <- floor(min(x)); max <- ceiling(max(x))
if(length(knots) == 1 & is.integer(knots)) {
cut(x, knots + 1, right = FALSE, include.lowest = TRUE)
} else {
cut(x, c(min, knots, max), right = FALSE, include.lowest = TRUE)
}
}
# example use:
# make_ind(1:10, 3)
# make_ind(1:10, 3L)
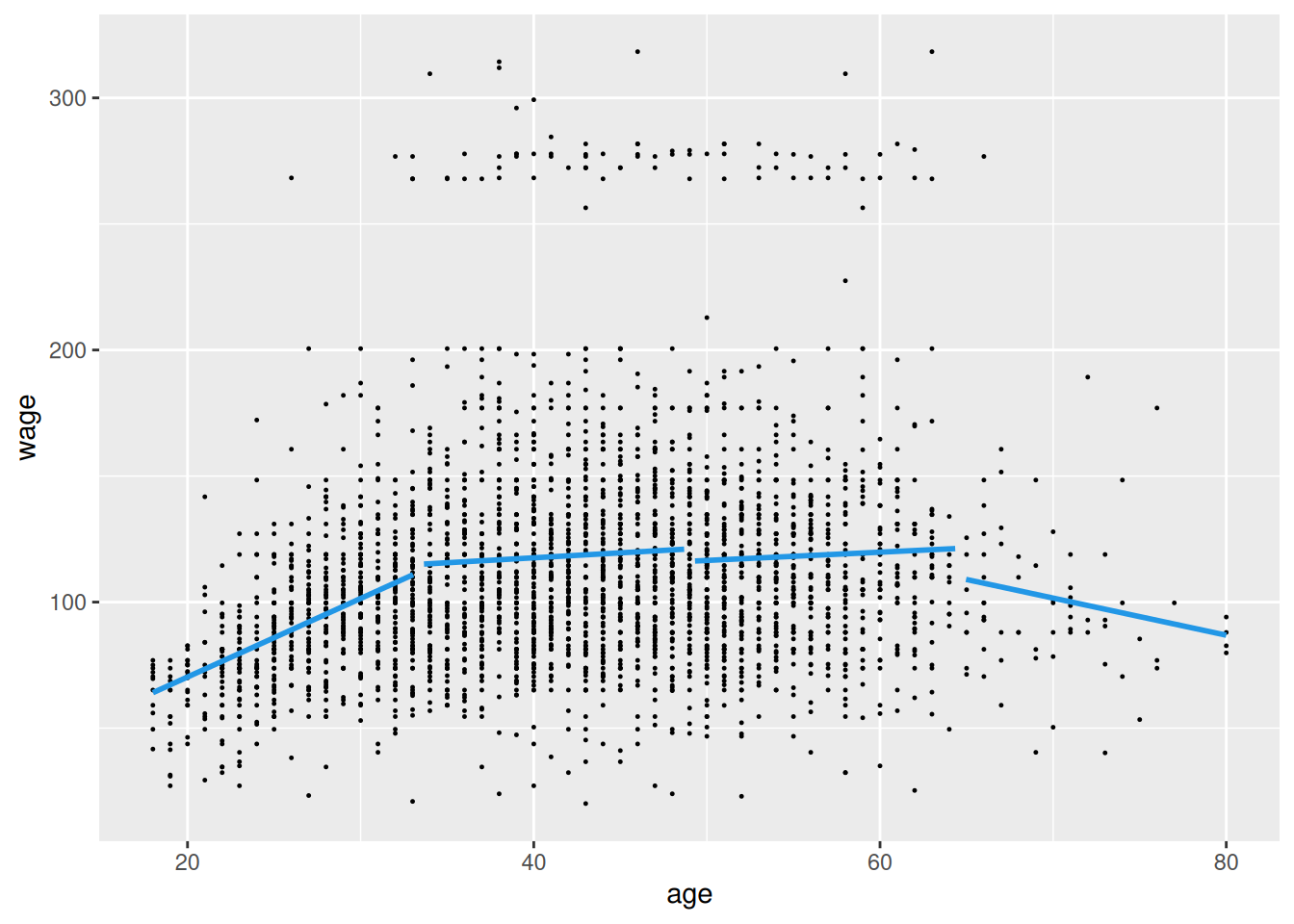
fit1 <- dat |>
dplyr::mutate(ind = make_ind(age, 3L) |> as.factor()) |>
lm(wage ~ ind*age, data = _)
grid |>
transform(ind = make_ind(age, 3L)) |>
modelr::add_predictions(fit1, var = "wage") |>
ggplot() + aes(x = age, y = wage) +
geom_point(data = dat, size = 0.2) +
geom_line(aes(group = ind), linewidth = 1, color = 4)
# --- continuous ---
# function to round a vector as much as possible while keeping elements distinguishable
# in: x - numeric vector
# add - integer, number of digits by which to increase precision (or decrease if negative)
# out: numeric vector
round_but_keep_different <- function(x, add = 0) {
x |> diff() |> abs() |> min() |> log10() |> (`-`)() |> ceiling() |> (`+`)(add) |>
round(x, digits = _)
}
# example use:
# c(1.2345, 1.2456, 1.2356) |> round_but_keep_different(add=0) # (1.23 1.25 1.24)
# c(1.2345, 1.2456, 1.2356) |> round_but_keep_different(add=1) # (1.234 1.246 1.236)
# function to apply truncated linear basis function to predictor
# in: x - numeric vector, values of predictor
# knots - numeric vector of breaks (without extremes)
# - single integer, number of interior breaks
# out: data frame, one column for each knot
make_max <- function(x, knots) {
if(length(knots) == 1 & is.integer(knots)) {
knots <- seq(min(x), max(x), length.out = knots + 2) |> head(-1) |> tail(-1)
}
out <- sapply(knots, function(k) pmax(0, x - k)) |> data.frame()
setNames(out, paste0("max(",round_but_keep_different(knots, add=1),")"))
}
# example use:
# make_max(1:10, 3L)
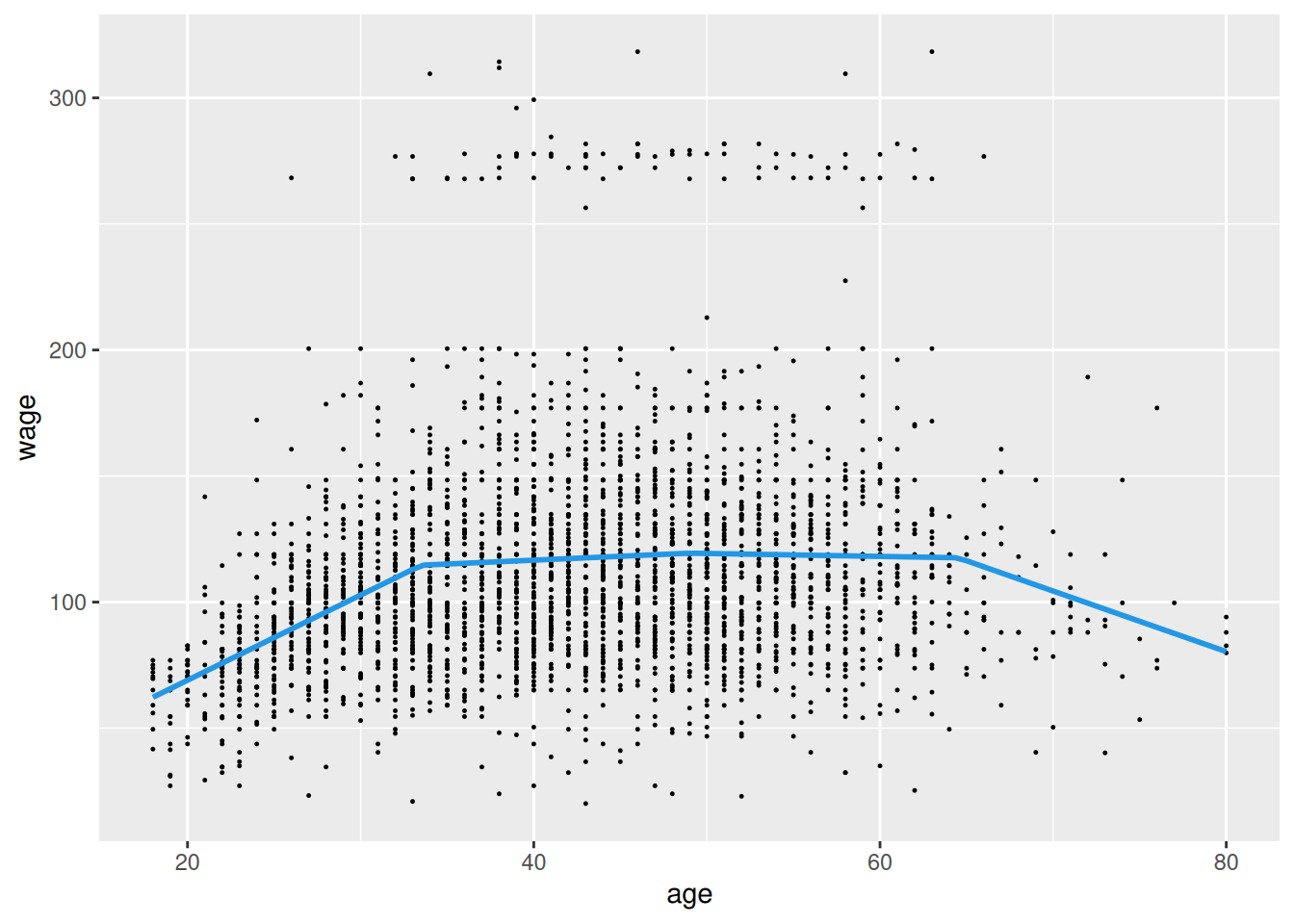
fit2 <- cbind(dat[c("wage","age")], make_max(dat$age, 3L)) |>
lm(wage ~ ., data = _)
grid |>
(\(df) cbind(df, make_max(df$age, 3L)))() |>
modelr::add_predictions(fit2, var = "wage") |>
ggplot() + aes(x = age, y = wage) +
geom_point(data = dat, size = 0.2) +
geom_line(linewidth = 1, color = 4)
# --- summary
fit1 |>
summary() |>
coef() |>
signif(2) |>
pander::pander()
fit2 |>
summary() |>
coef() |>
signif(2) |>
pander::pander()
| Estimate | Std. Error | t value | Pr(>|t|) | |
|---|---|---|---|---|
| (Intercept) | 8 | 10 | 0.79 | 0.43 |
| ind[33.5,49) | 94 | 15 | 6.3 | 2.7e-10 |
| ind[49,64.5) | 92 | 20 | 4.5 | 7e-06 |
| ind[64.5,80.1] | 200 | 81 | 2.4 | 0.015 |
| age | 3.1 | 0.36 | 8.6 | 9.3e-18 |
| ind[33.5,49):age | -2.7 | 0.45 | -6.1 | 1.1e-09 |
| ind[49,64.5):age | -2.8 | 0.49 | -5.7 | 1e-08 |
| ind[64.5,80.1]:age | -4.6 | 1.2 | -3.8 | 0.00014 |
| Estimate | Std. Error | t value | Pr(>|t|) | |
|---|---|---|---|---|
| (Intercept) | 1.4 | 8.3 | 0.17 | 0.86 |
| age | 3.4 | 0.28 | 12 | 7.9e-33 |
max(34) |
-3.1 | 0.4 | -7.7 | 1.8e-14 |
max(49) |
-0.43 | 0.36 | -1.2 | 0.24 |
max(64) |
-2.3 | 0.91 | -2.5 | 0.012 |
Aby bol rozdiel v šírke pásu spoľahlivosti medzi kubickým a prirodzeným kubickým splajnom zjavnejší, súbor údajov o mzdách bol náhodne zredukovaný.
Iným prístupom k vystihnutiu nelineárneho vzťahu odozvy a prediktoru je obmedziť trénovaciu vzorku pre zvolený model na pozorovania z blízkeho okolia bodu x_0 (bodu predpovede). Presnejšie povedané, upraviť veľkosť vplyvu pozorovaní na odhad g(x) podľa blízkosti ku x_0.
Preto sa definuje váhová funkcia K(x_i,x), nazývaná tiež jadrová (kernel) funkcia, ktorá najvzdialenejším pozorovaniam x_i priradí nízku hodnotu (až nulu), a naopak blízkym pozorovaniam vysokú váhu.
Formálne je lokálne vážená regresná funkcia definovaná ako odhad \hat g(x) = \mathbf{b}(x)\cdot\hat{\boldsymbol\beta}(x_0), kde \mathbf{b}(x) je vektor bázových funkcií a parametre \boldsymbol\beta viazané na x_0 sú odhadnuté váženou metódou najmenších štvorcov, \hat{\boldsymbol\beta}(x_0) = \underset{\boldsymbol\beta(x_0)}{\operatorname{argmin}} \sum_{i=1}^n\underbrace{\frac{K(x_i,x_0)}{\sum_{j=1}^nK(x_j,x_0)}}_{\text{normovaná váha}}\ \Big(y_i-g(x_i)\Big)^2.
To znamená, že pre výpočet každej jednej predikcie je nutné odhadnúť model nanovo. Preto lokálna regresia patrí medzi metódy založené na pamäti (memory-based).
Pri lokálnej regresii je potrebné zvoliť:
Jadrová funkcia funkcia sa najčastejšie volí ako
Ak je napr. jadrová funkcia definovaná tak, že priradí nenulovú a rovnakú váhu iba k najbližším pozorovaniam, a g je konštantná funkcia, potom dostávame tzv. regresnú metódu k-najbližších susedov.
fit1 <- lm(wage ~ splines::ns(year, df = 4) + splines::ns(age, df = 5) + education,
data = ISLR2::Wage)
fit1 |> coef() (Intercept) splines::ns(year, df = 4)1
46.949491 8.624692
splines::ns(year, df = 4)2 splines::ns(year, df = 4)3
3.762266 8.126549
splines::ns(year, df = 4)4 splines::ns(age, df = 5)1
6.806473 45.170123
splines::ns(age, df = 5)2 splines::ns(age, df = 5)3
38.449704 34.239237
splines::ns(age, df = 5)4 splines::ns(age, df = 5)5
48.677634 6.557265
education2. HS Grad education3. Some College
10.983419 23.472889
education4. College Grad education5. Advanced Degree
38.313667 62.553971 gam::plot.Gam(fit1, se = TRUE, col = 4)
lm(wage ~ year + splines::ns(age, 5) + education, data = ISLR2::Wage) |>
anova(fit1)Analysis of Variance Table
Model 1: wage ~ year + splines::ns(age, 5) + education
Model 2: wage ~ splines::ns(year, df = 4) + splines::ns(age, df = 5) +
education
Res.Df RSS Df Sum of Sq F Pr(>F)
1 2989 3694885
2 2986 3691919 3 2966.4 0.7997 0.4939library(gam) # necessary to load due to inaccountable behaviour of "gam::s" in gam() formula
gam::gam(wage ~ s(year, df = 4) + s(age, df = 5) + education,
data = ISLR2::Wage) |>
anova() # summary()Anova for Nonparametric Effects
Npar Df Npar F Pr(F)
(Intercept)
s(year, df = 4) 3 1.086 0.3537
s(age, df = 5) 4 32.380 <2e-16 ***
education
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1span (podiel okolia x_0 na celkovom počte pozorovaní) sa interne použije funkcia stats::loess.gam::gam(wage ~ year + lo(age, span = 0.3) + education,
data = ISLR2::Wage) |>
plot.Gam(se = TRUE, col = 4)
