plot(am ~ wt, mtcars, pch=20, xlim = c(1,6), ylim = c(-0.3,1.3))
lm(am ~ wt, mtcars) |> abline(reg = _, col = 4, lwd = 2)
legend("topright",
legend = c("data", "y=1.5-0.35x"),
pch=c(20,NA), lty=c(0,1), col=c(1,4), lwd = c(NA,2)
)
plot(am ~ wt, mtcars, pch=20, xlim = c(1,6), ylim = c(-0.3,1.3))
plot(function(x) exp(15-5*x)/(1+exp(15-5*x)), from = 1, to = 6, add=T, col = 4, lwd=2)
abline(h = 0.5, lty="dashed")
abline(a = 15/4+1/2, b=-5/4, lty="dotted", col = 4)
abline(v = 15/5, lty="dotted", col = 4)
legend("topright",
legend = c("data", expression(paste(b[1]==15,", ", b[2]==-5))),
pch=c(20,NA), lty=c(0,1), col=c(1,4), lwd = c(NA,2)
)
fit <- glm(am ~ wt, mtcars, family = "binomial")
fit
Call: glm(formula = am ~ wt, family = "binomial", data = mtcars)
Coefficients:
(Intercept) wt
12.040 -4.024
Degrees of Freedom: 31 Total (i.e. Null); 30 Residual
Null Deviance: 43.23
Residual Deviance: 19.18 AIC: 23.18xgrid <- seq(1,6,0.1)
plot(am ~ wt, mtcars, pch=20)
lines(xgrid,
predict(fit, newdata = data.frame(wt = xgrid), type = "response"),
col = 4, lwd = 2)
legend("topright",
legend = c("data", expression(paste(b[1]==12,", ", b[2]==-4))),
pch=c(20,NA), lty=c(0,1), col=c(1,4), lwd = c(NA,2)
)
# odhad
fit <- nnet::multinom(Species ~ Petal.Width, data = iris, trace = FALSE)
# rozdelenie údajov
ggplot(iris) + aes(x = Petal.Width, y = Species) +
geom_boxplot(varwidth = T)
# súhrn modelu
fitCall:
nnet::multinom(formula = Species ~ Petal.Width, data = iris,
trace = FALSE)
Coefficients:
(Intercept) Petal.Width
versicolor -24.08868 31.44849
virginica -45.20657 44.39249
Residual Deviance: 33.44131
AIC: 41.44131 # zobrazenie pravdepodobností
predict(fit, type = "probs") |>
as.data.frame() |>
transform(Petal.Width = iris$Petal.Width) |>
tidyr::pivot_longer(cols = -Petal.Width, names_to = "Species", values_to = "Prob") |>
ggplot() + aes(x = Petal.Width, y = Prob, color = Species, group = Species) +
geom_line()
# klasifikácia
iris |>
transform(fit = predict(fit, type = "class")) |>
ggplot() + aes(x = Petal.Width) +
geom_point(aes(y = Species)) +
geom_line(aes(y = fit), color = 4, lwd = 1)
fit <- mtcars |>
dplyr::mutate(cyl = ordered(cyl, c("4","6","8"))) |>
MASS::polr(cyl ~ disp, data=_)Warning: glm.fit: fitted probabilities numerically 0 or 1 occurredfitCall:
MASS::polr(formula = cyl ~ disp, data = dplyr::mutate(mtcars,
cyl = ordered(cyl, c("4", "6", "8"))))
Coefficients:
disp
0.4443344
Intercepts:
4|6 6|8
64.9643 118.0268
Residual Deviance: 3.924663
AIC: 9.924663
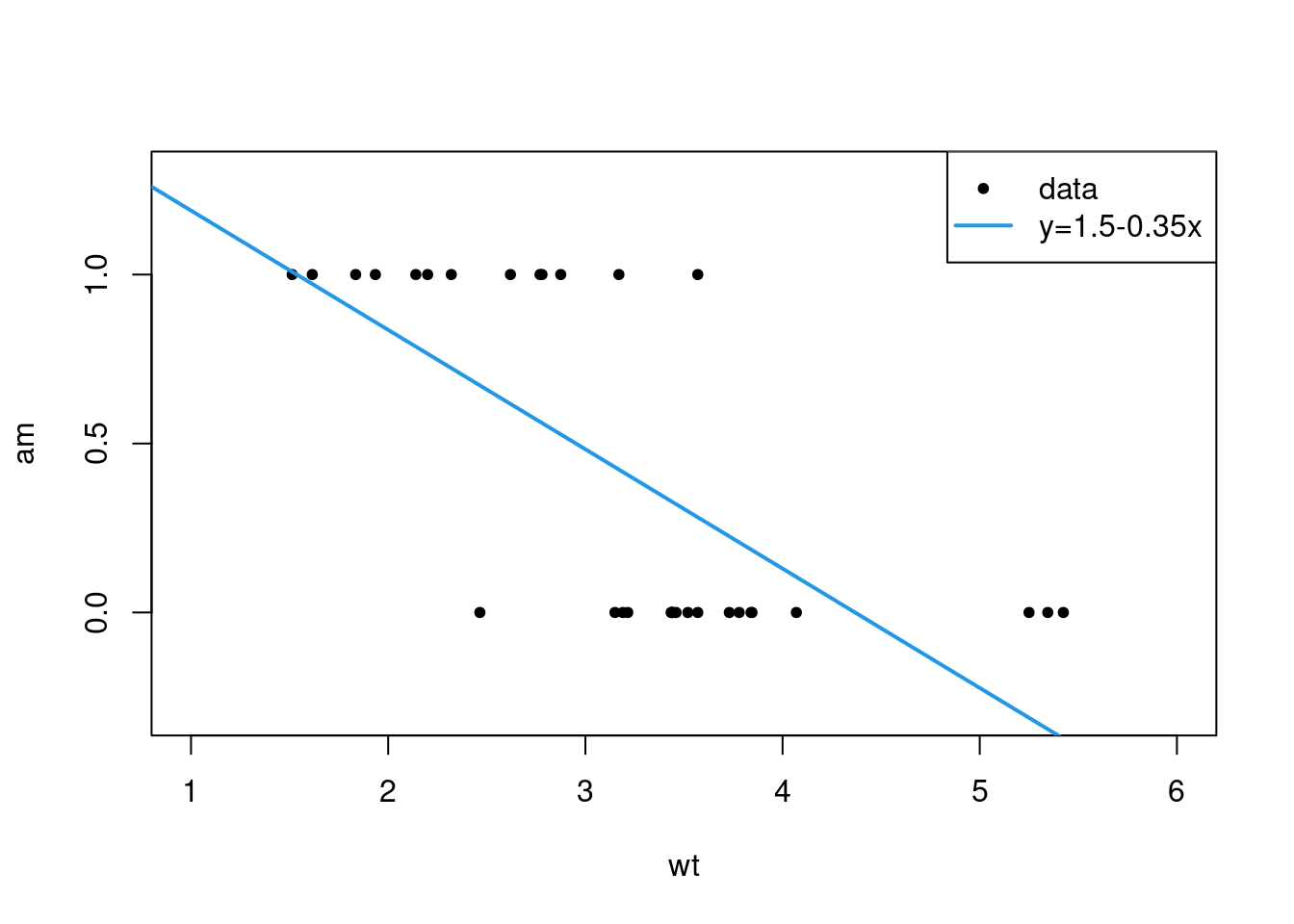
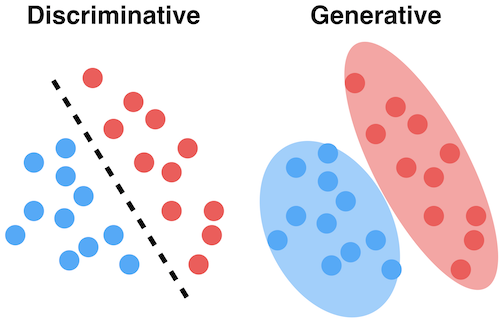
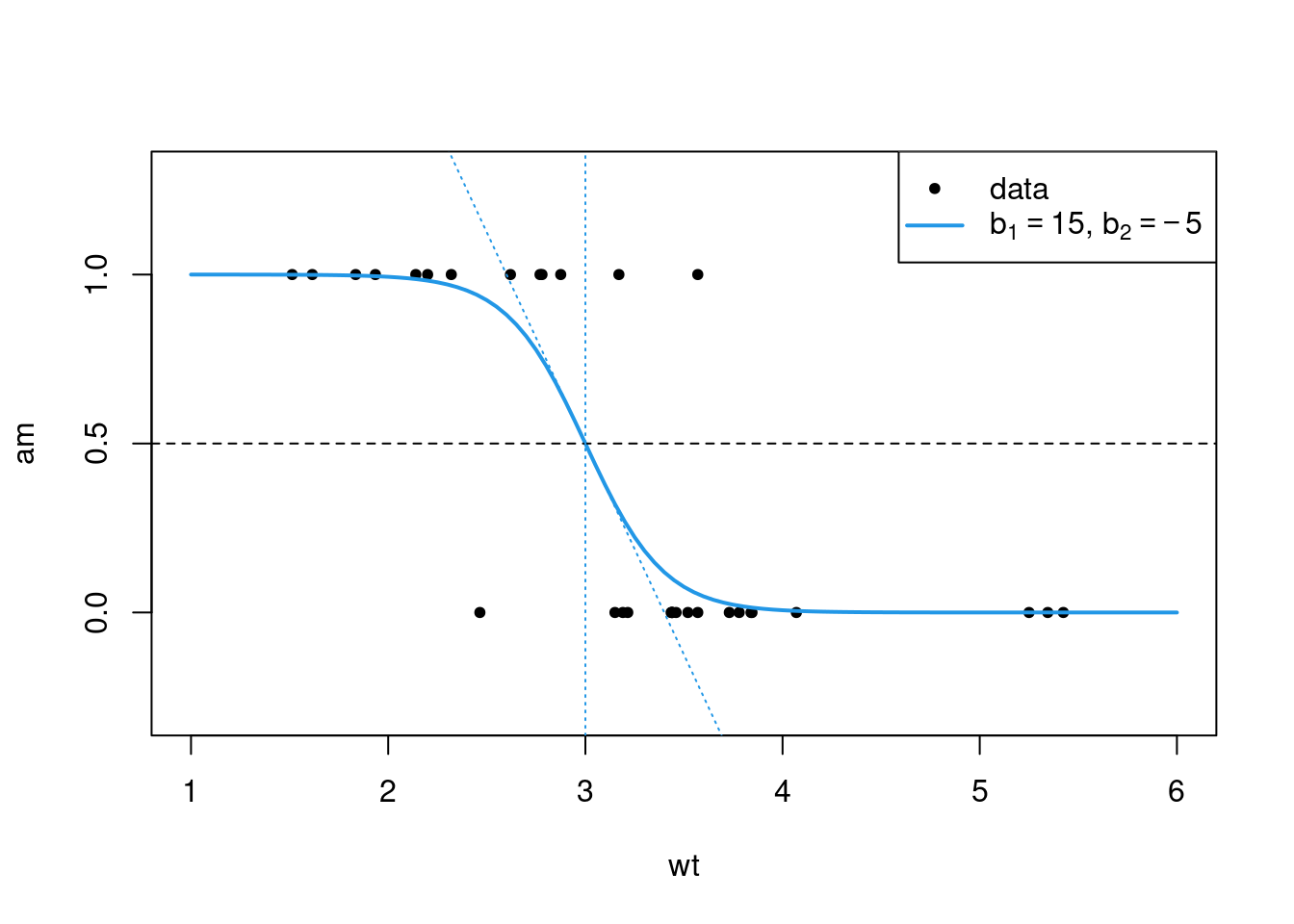
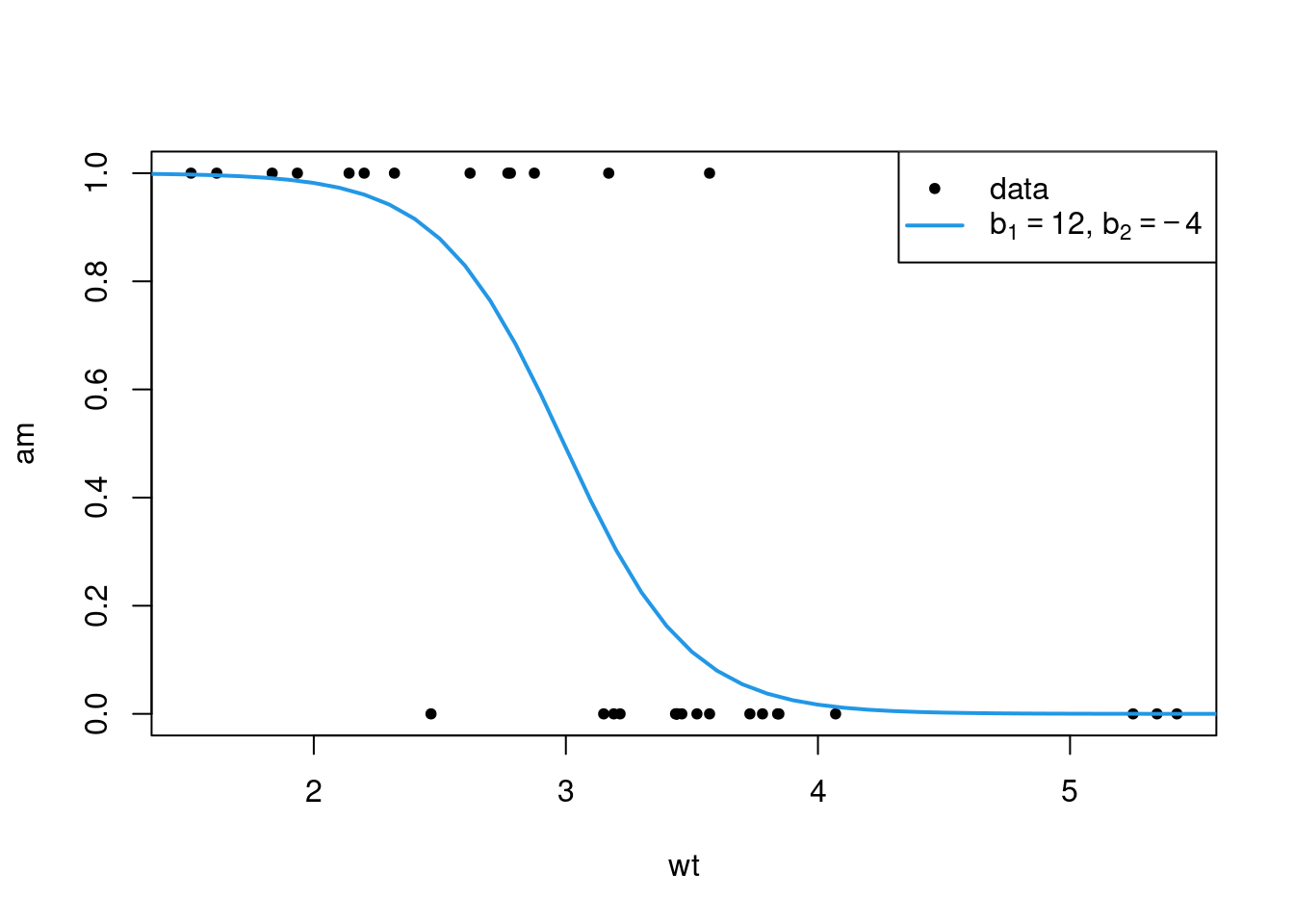
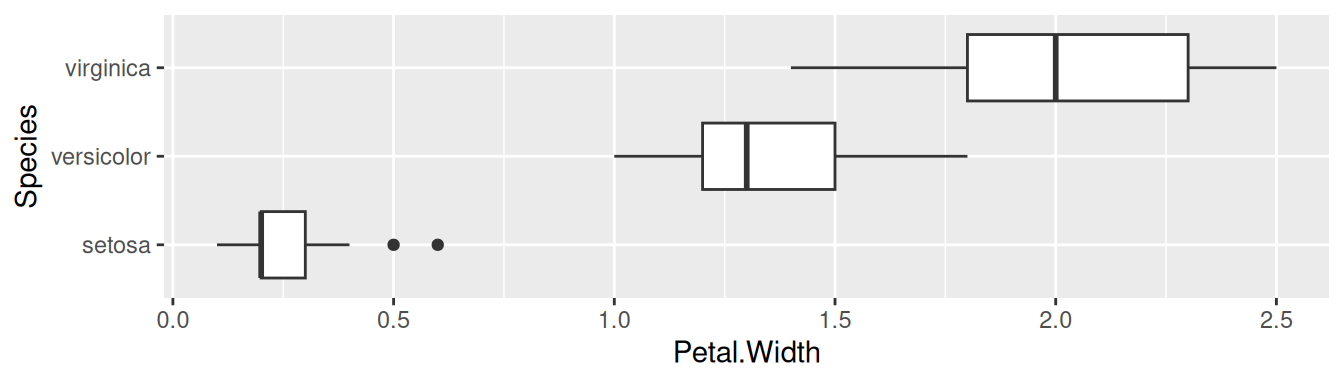
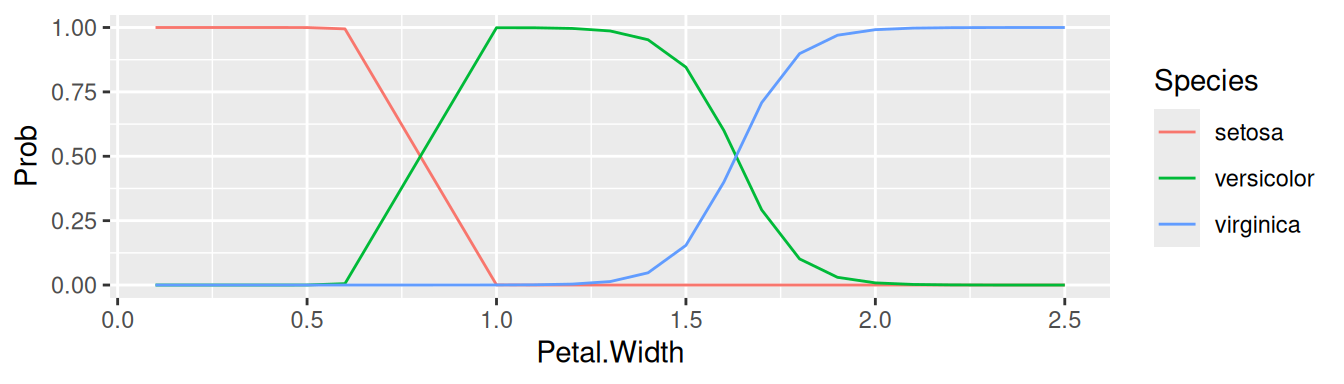
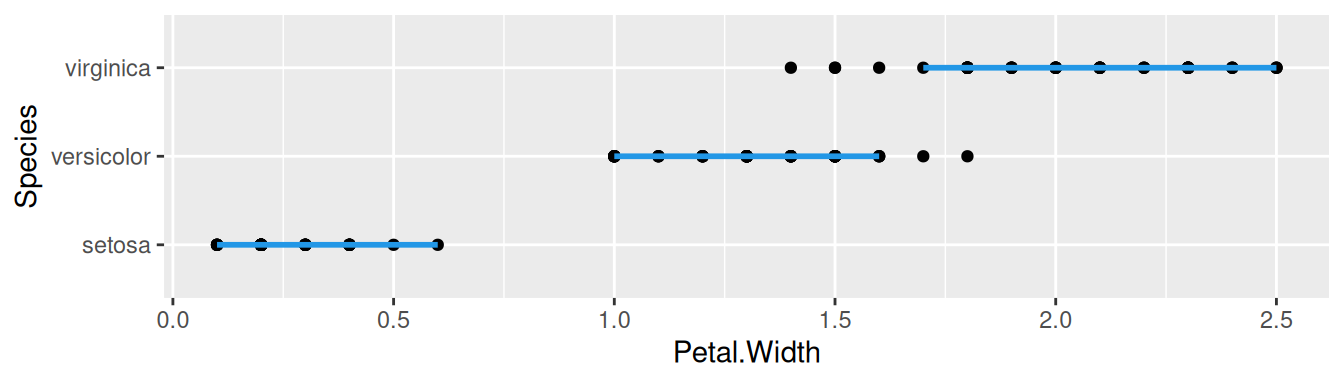
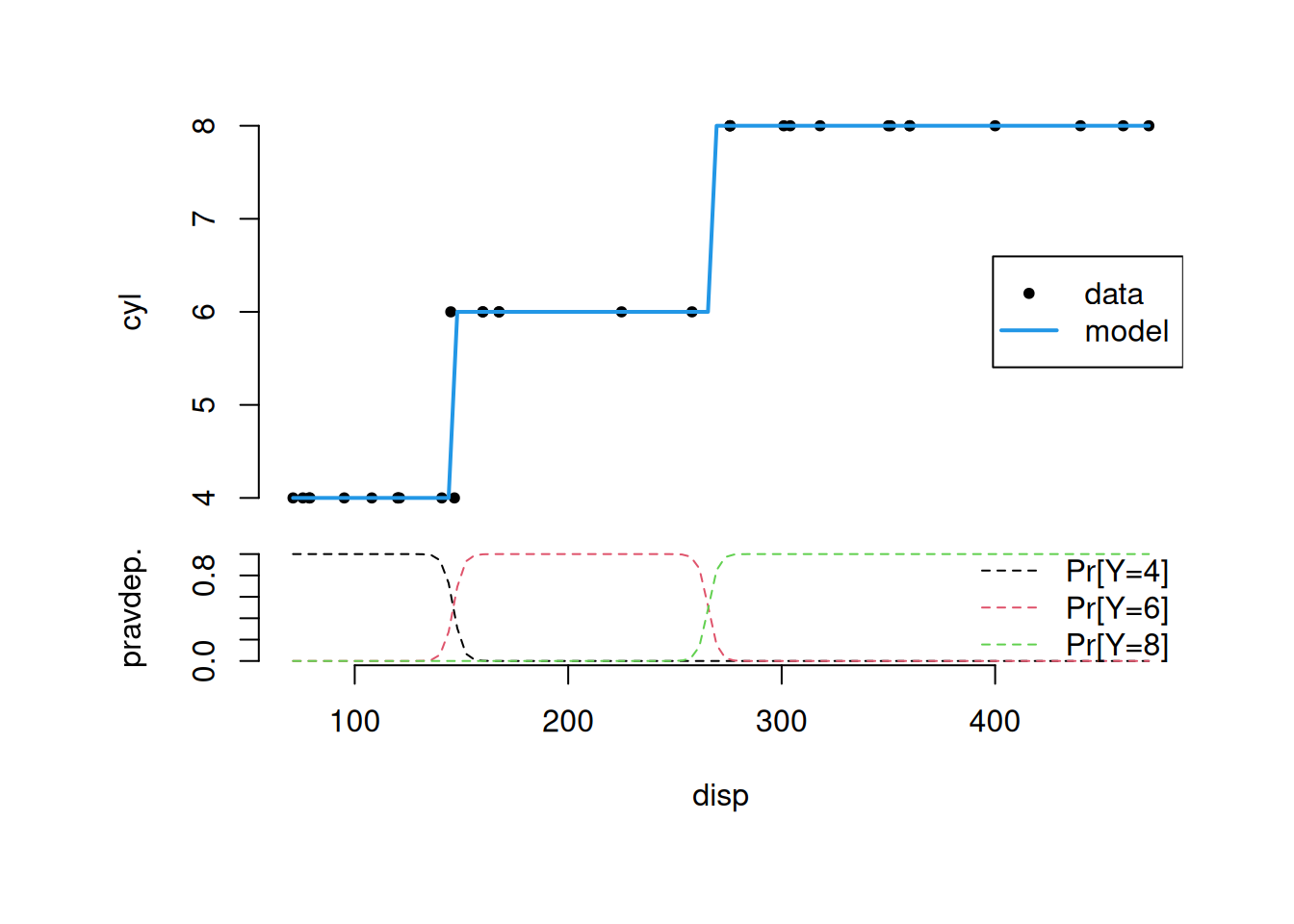
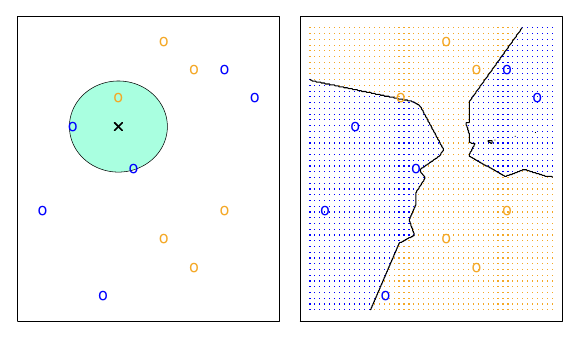
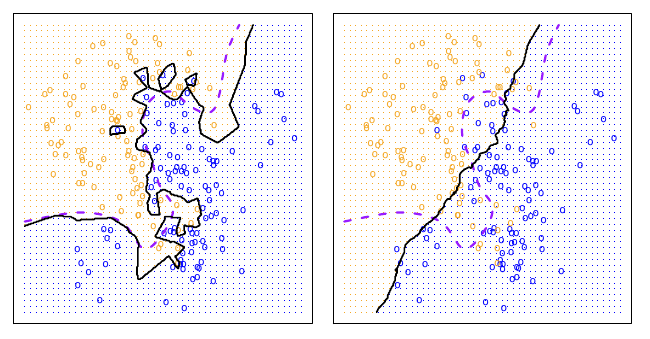
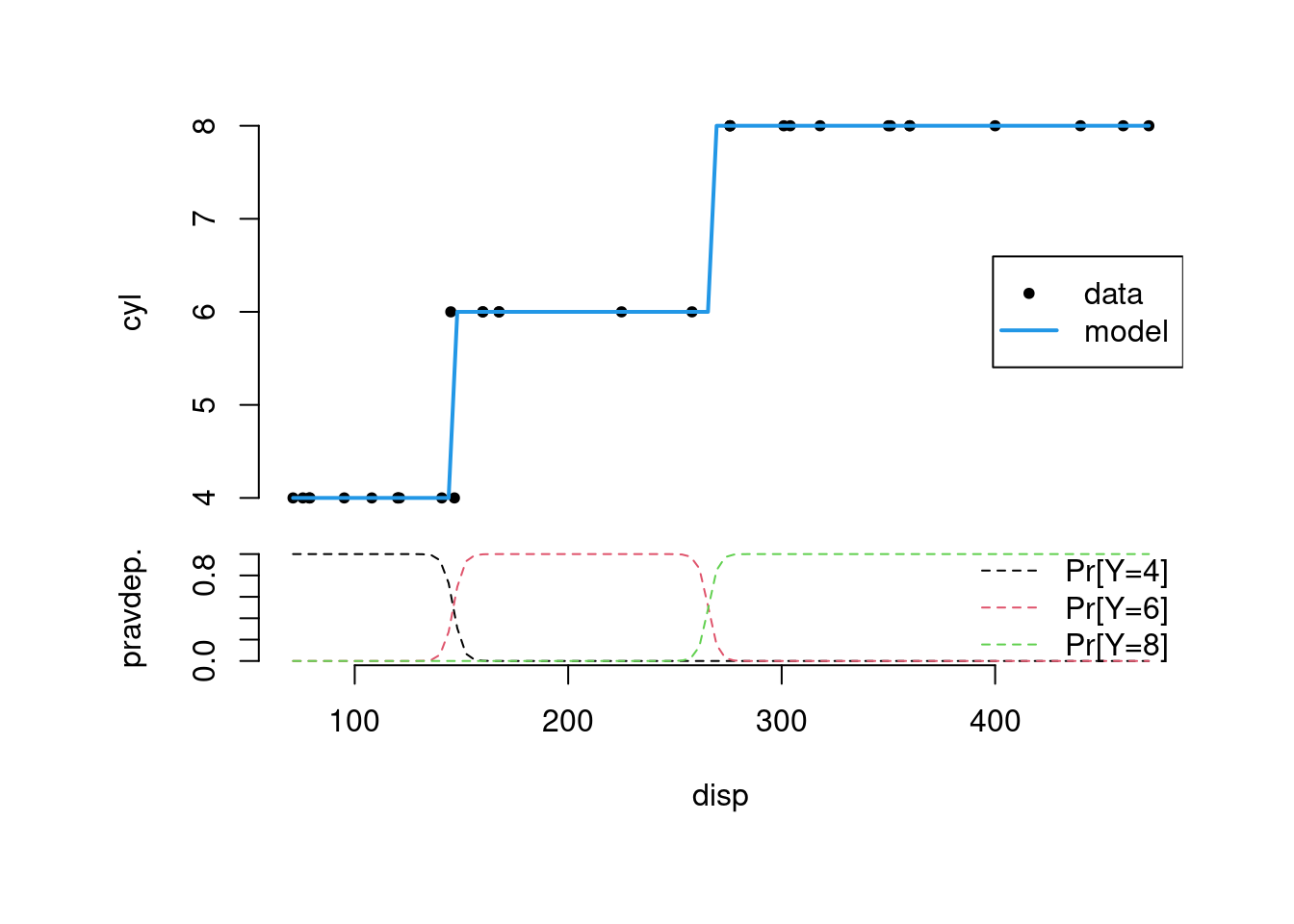
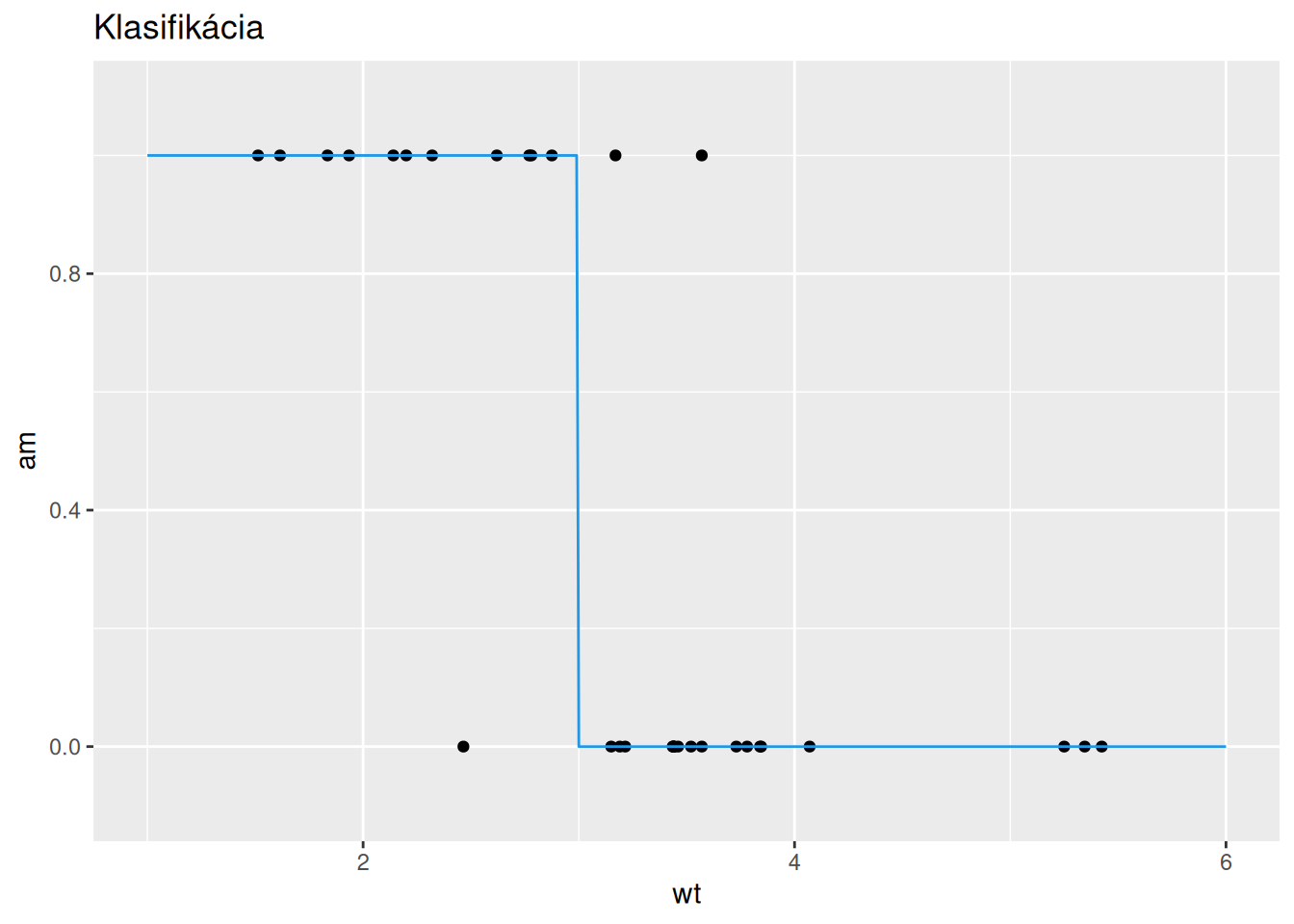
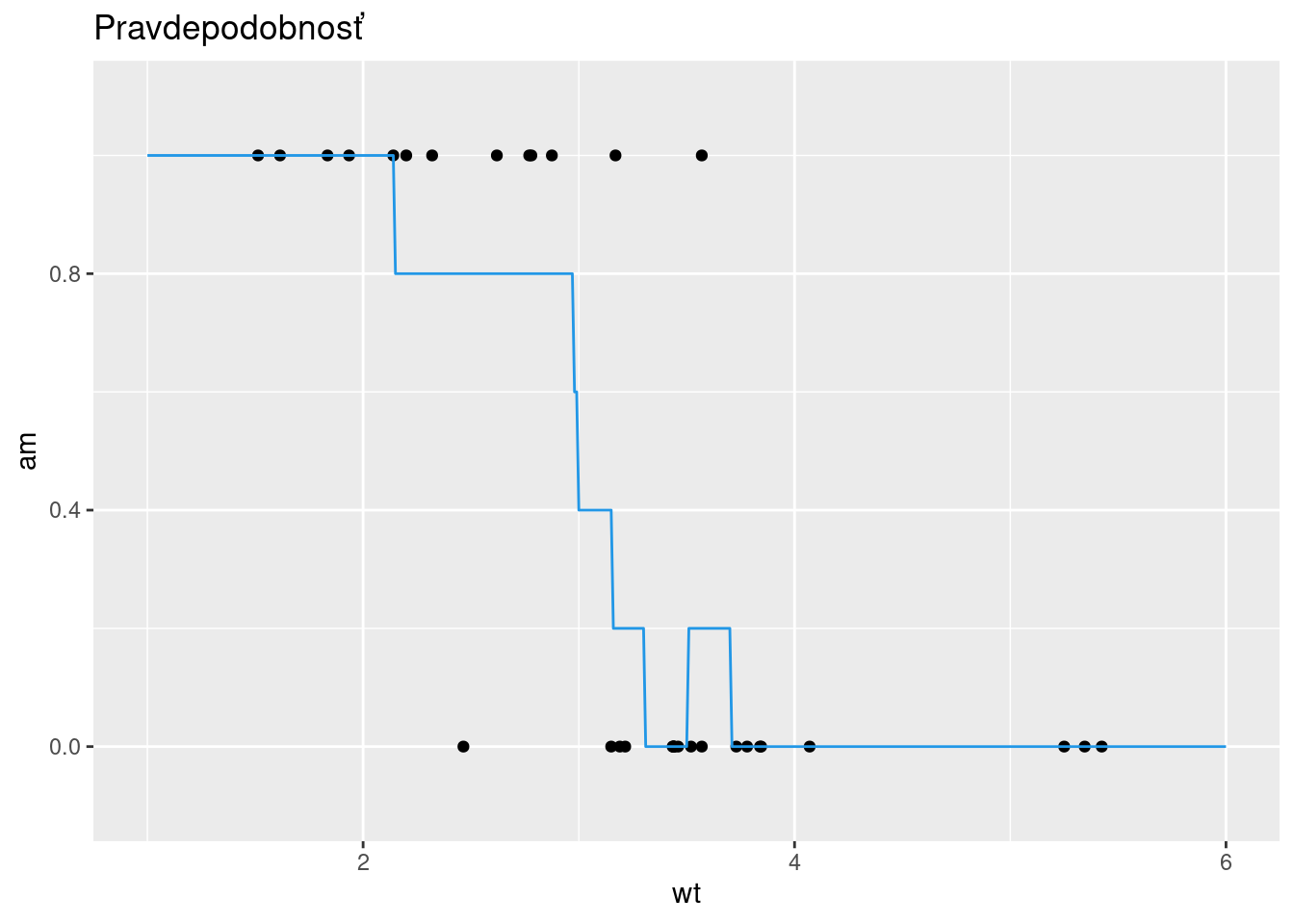
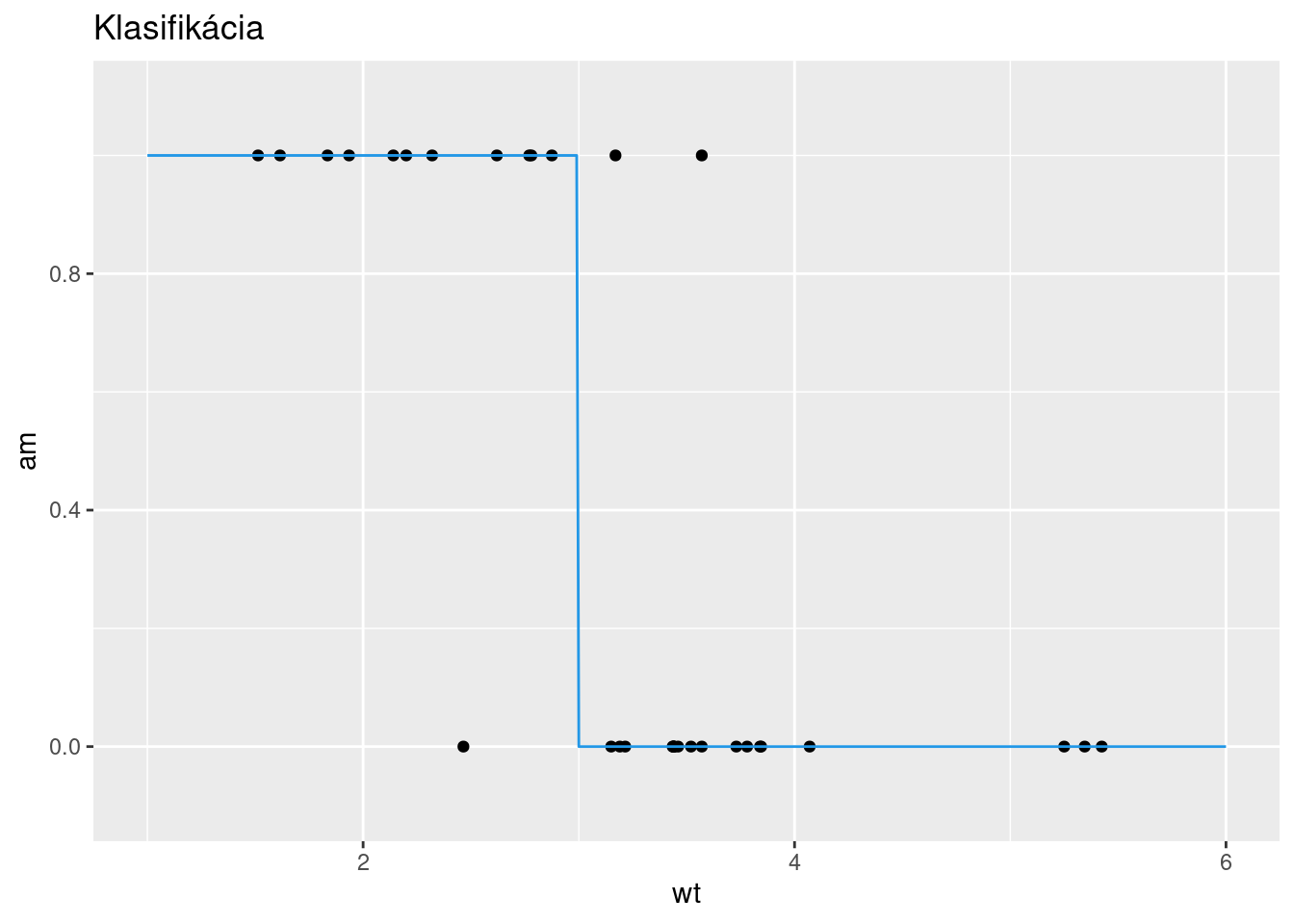
Warning: did not converge as iteration limit reachedxnew <- seq(min(mtcars$disp), max(mtcars$disp), length.out = 100)
layout(rbind(1,2), heights = c(5,3))
old <- par(oma=c(3, 3, 3, 3), mar=c(1, 4, 0, 0))
plot(cyl ~ disp, mtcars, axes=F, pch=20)
lines(x = xnew,
y = as.numeric(as.character(predict(fit, newdata = list(disp = xnew)))),
col = 4, lwd=2)
legend("right", c("data","model"), lty=c(NA,1), lwd=c(NA,2), col=c(1,4), pch = c(20,NA))
axis(2); par(mar=c(4, 4, 0, 0))
matplot(xnew, predict(fit, newdata = list(disp = xnew), type = "p"),
xlab = "disp", ylab = "pravdep.", type= "l", lty = 2, axes = F)
legend("right", c("Pr[Y=4]","Pr[Y=6]","Pr[Y=8]"), lty=2, col=1:3, bty="n")
axis(1); axis(2)
layout(rbind(1))
par(old)
Jeden prediktor, dve triedy, dataset mtcars.
# Funkcia na výpočet podmienených pravdepodobností:
knn.prob <- Vectorize(
FUN = function(x, vx, vy, k) {
x |> (`-`)(vx) |> abs() |> sort(index.return=T) |> getElement("ix") |> head(k) |> (`[`)(x=vy, i=_) |> mean()
},
vectorize.args = "x"
)
# použitie: knn.prob(6, mtcars$wt, mtcars$am, k=5)
# klasifikácia a výpočet pravdepodobností:
pred <- data.frame(wt = seq(1,6,0.01)) |>
transform(
clas = class::knn(train = cbind(mtcars$wt), # prediktory (ako matica plánu)
test = cbind(wt), # nové hodnoty prediktorov
cl = as.factor(mtcars$am), # odozva (triedy)
k = 5 # počet susedov, floor(sqrt(nrow(mtcars)))
) |> as.character() |> as.numeric(), # factor to number
prob = knn.prob(wt, vx = mtcars$wt, vy = mtcars$am, k = 5)
)
# zobrazenie:
ggplot(mtcars) + aes(x = wt) + geom_point(aes(y = am)) +
geom_line(aes(y = prob), data = pred, color = 4) +
ggtitle("Pravdepodobnosť") +
ylim(-0.1, 1.1)
ggplot(mtcars) + aes(x = wt) + geom_point(aes(y = am)) +
geom_line(aes(y = clas), data = pred, color = 4) +
ggtitle("Klasifikácia") +
ylim(-0.1, 1.1)
# trénovanie (k=9 zvolené pomocou resamplingu)
fit <- caret::train(Species ~ Petal.Length + Petal.Width, data = iris,
method = "knn",
preProcess = c("center", "scale")
)
# predpovede a zobrazenie
xgrid <- expand.grid(Petal.Length = seq(0.8,7.2,0.05),
Petal.Width = seq(0,2.7,0.05))
fit |>
predict(newdata = xgrid, "prob") |>
cbind(xgrid) |>
dplyr::select(-setosa, -virginica) |>
dplyr::rename(prob_versicolor = versicolor) |>
ggplot() + aes(x = Petal.Length, y = Petal.Width) +
geom_contour_filled(aes(z = prob_versicolor, colour = prob_versicolor), alpha = 0.5) +
geom_point(aes(shape = Species), data = iris) + ggtitle("Pravdepodobnosť pre versicolor")
fit |>
predict(newdata = xgrid, "raw") |>
cbind(Species = _, xgrid) |>
ggplot() + aes(x = Petal.Length, y = Petal.Width) +
geom_tile(aes(fill = Species), alpha = 0.3) +
geom_point(aes(color = Species), data = iris) +
ggtitle("Klasifikácia")
