11 Model združeného rozdelenia a aplikácie
11.1 Modelovanie združeného rozdelenia
- Empirická distribučná funkcia \hat F_n je (nevychýleným) neparametrickým odhadom združenej CDF, \hat F_n(\mathbf{x}) = \frac1n\sum_{i=1}^n\prod_{j=1}^p I(x_{ij}\leq x_j) kde x_j je prvok argumentu a x_{ij} značí i-te pozorovanie j-tej náhodnej premennej (prvok matice pozorovaní \mathbf{X}).
- Jadrovo vyhladená hustota, s jadrovou funkciou definovanou (pre jednoduchosť) napr. ako súčin jednorozmerných jadrových funkcií K_j so šírkou pásma h_j, je daná vzťahom
\hat f(\mathbf{x}) = \frac1{n\prod_{j=1}^ph_j}\sum_{i=1}^n\prod_{j=1}^pK_j\left(\frac{x_j - x_{ij}}{h_j}\right)
Delenie šírkou pásma zaručuje, že určitý integrál (plocha pod funkciou) f bude 1.
- Výhodou jadrového odhadu rozdelenia je v tom, že máme hladkú funkciu, ktorú možno derivovať. Nevýhodou je výpočtová náročnosť (najmä odhad šírky pásma) so vzrastajúcim p – jav známy ako kliatba rozmernosti.
- Kliatbe rozmernosti sa pri modelovaní dá vyhnúť špeciálnymi predpokladmi. Parametrické modely zavádzajú pomerne silné predpoklady o tom, ako rozdelenie vyzerá, takže stačí už len určiť parametre. Menej drastické sú predpoklady o nejakom druhu štruktúry prítomnej v rozdelení, ktoré využívajú metódy ako PCA, faktorové modely, zmesi rozdelení či grafické modely (predp. nezávislosť).
- Pre veľa jednorozmerných parametrických tried rozdelení existuje rozšírenie na náhodný vektor, napr. hustota združeného normálneho rozdelenia je definovaná f(\mathbf{x}) = \frac{1}{\sqrt{(2\pi)^p|\mathbf{\Sigma}|}}e^{-\frac12(\mathbf{x}-\boldsymbol{\mu})^T\mathbf{\Sigma}^{-1}(\mathbf{x}-\boldsymbol{\mu})} kde \mathbf{\Sigma} je kovariančná matica, takže \Sigma_{ij}=cov[X_i,X_j].
- Kompozitný model umožňuje rozložiť analýzu rozdelenia náhodného vektora zvlášť na okrajové rozdelenia a zvlášť na vzťahy medzi premennými.
11.2 Rozklad združeného rozdelenia
- Nevýhoda zovšeobecnení jednorozmerných rozdelení do väčšieho rozmeru spočíva v tom, že marginálne rozdelenia takého združeného rozdelenia sú všetky z rovnakej triedy.
- Ak chceme modelovať stochastickú závislosť bez ohľadu na individuálne vlastnosti náhodných premenných, musíme združené rozdelenie reprezentovať ako marginálie zviazané kopulou. V reči distribučných funkcií, resp. funkcií hustoty sa rozklad zapíše \begin{split} F(x_1,\ldots,x_p) &= C\Big(F_1(x_1), \ldots, F_p(x_p)\Big) \\ f(x_1,\ldots,x_p) &= c\Big(F_1(x_1), \ldots, F_p(x_p)\Big)\cdot f_1(x_1)\cdot\ldots\cdot f_p(x_p) \end{split} kde C je kopula náhodného vektora \vec X, a c je jej hustota.
\qquad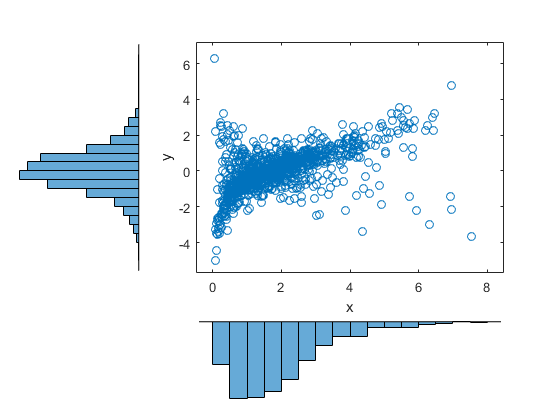 
\longrightarrow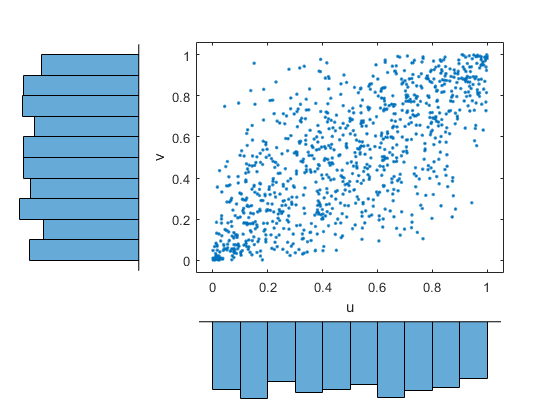 
- Transformované náhodné premenné U_i=F_i(X_i) majú rovnomerné rozdelenie na intervale [0,1].
- Výpočet podmienenej združenej CDF je s kopulami jednoduchší, F_{p|-p}(x_p|\vec x_{-p}) = \frac{\int\limits_{-\infty}^{x_p}f(x_1,...,x_{p-1},t)dt}{\int\limits_{-\infty}^{\infty}f(x_1,...,x_{p-1},t)dt} = \frac{\int\limits_0^{F_p(x_p)}c\Big(F_1(x_1),...,F_{p-1}(x_{p-1}),s\Big)ds}{\int\limits_{0}^{1}c\Big(F_1(x_1),...,F_{p-1}(x_{p-1}),s\Big)ds} kde bola pri úprave použitá substitúcia s=F_p(t), takže člen ds=f_p(t)dt v čitateli a menovateli sa eliminoval spolu s ostatnými marginálnymi hustotami.
11.3 Kopula
- Vlastnosti:
- C(u_1,\ldots,u_p)=0 pre ľubovoľné u_i=0,
- C(1,\ldots,1,u_i,1\ldots,1)=u_i, \forall i\in\{1,\ldots,p\},
- C je p-rastúca funkcia, čo pre p=2 znamená C(v_1,v_2)-C(v_1,u_2)-C(u_1,v_2)+C(u_1,u_2)\geq0, pričom u_i\leq v_i.
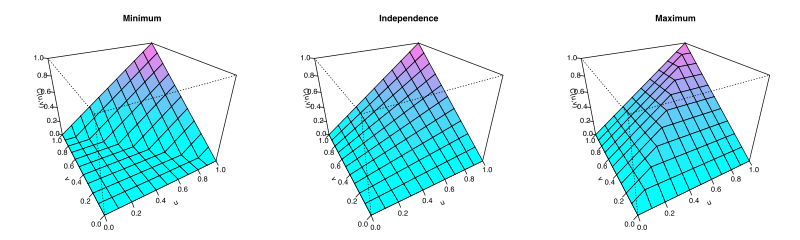
- Špeciálnymi prípadmi sú kopule M,\Pi,W, ktoré predstavujú
- úplnú negatívnu závislosť, W(u_1,u_2)=\max(0, u_1+u_2-1),
- nezávislosť, \Pi(u_1,\ldots,u_p)=u_1\cdot\ldots\cdot u_p
- úplnú závislosť, M(u_1,\ldots,u_p)=\min(u_1,\ldots,u_p),
- Graf špeciálnych kopúl W, \Pi, M:
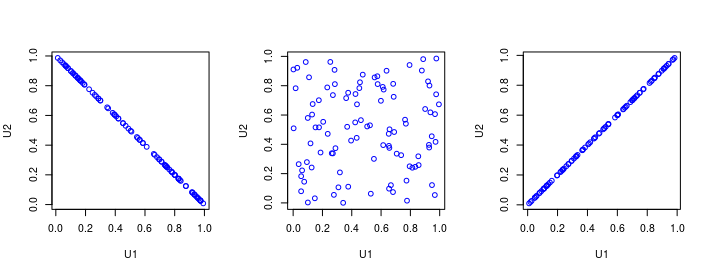
- Bodové grafy náhodných výberov simulovaných z kopúl W, \Pi, M:
11.4 Využitie modelu závislosti
Kopula C teda predstavuje tú časť združeného rozdelenia, ktorá popisuje závislosť medzi premennými.
Pomocou modelu závislosti môžeme
- skúmať vlastnosti vzťahu ako napr. závislosť v extrémoch (tail dependence) či rôzne (a)symetrie,
- určovať pravdepodobnosť, že premenné (ne)prekročia kritickú hodnotu,
- vypočítať kvantily, ktoré (ne)budú prekročené s danou pravdepodobnosťou.
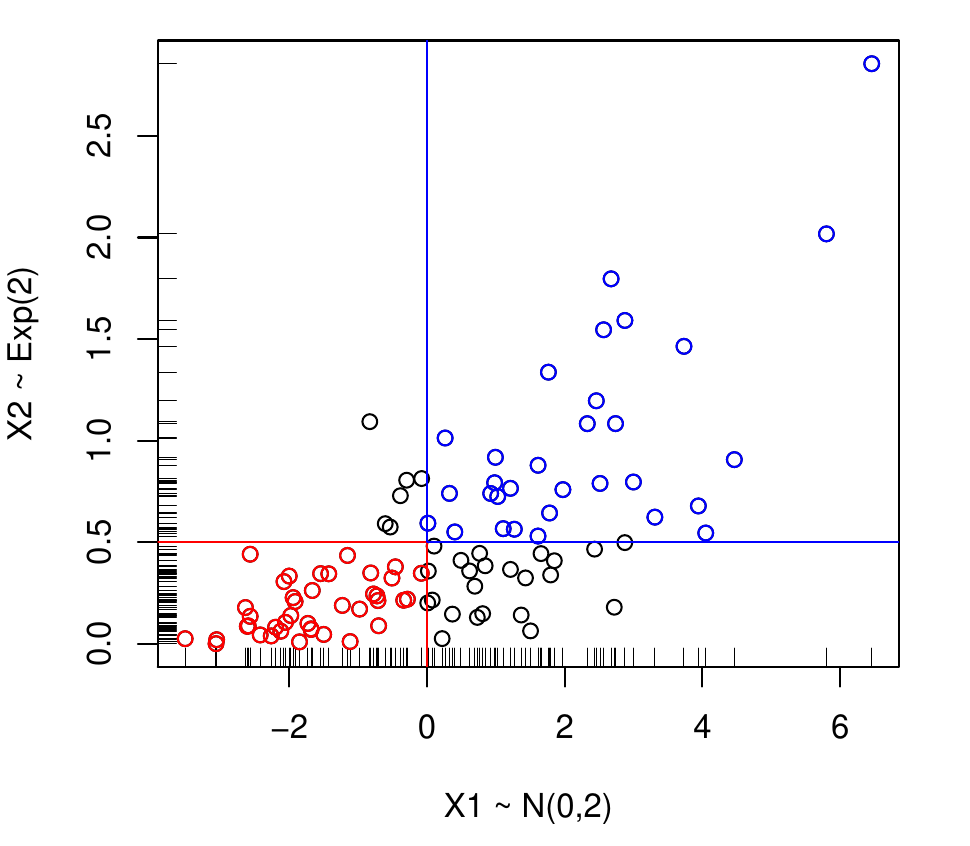
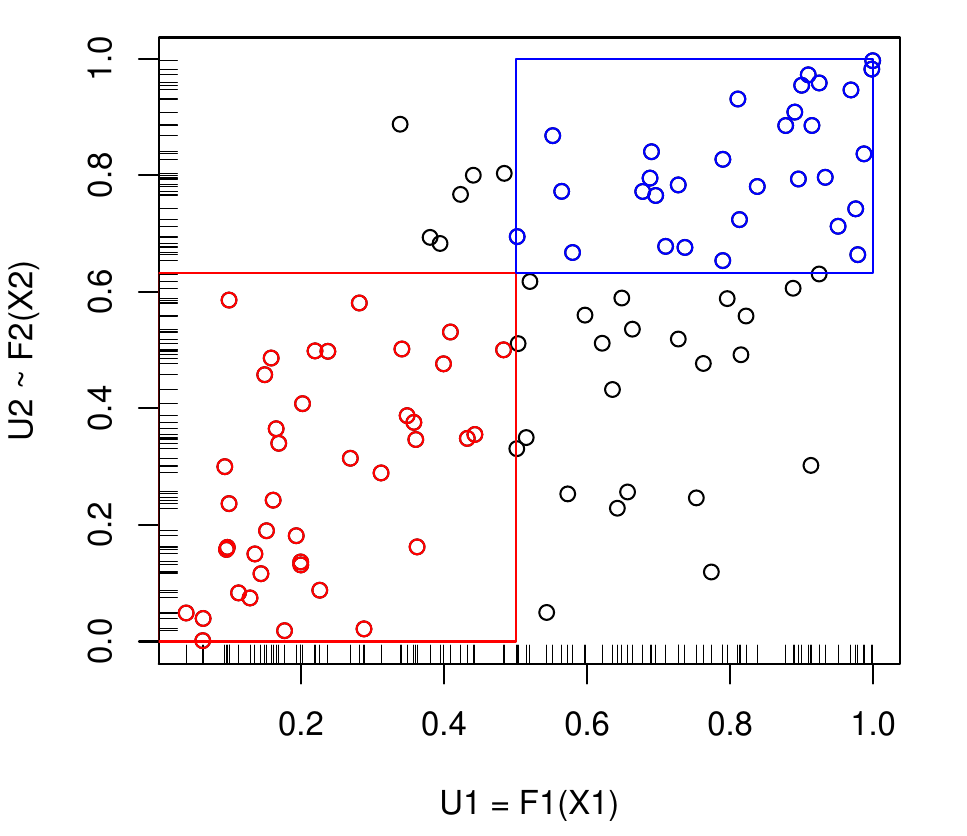
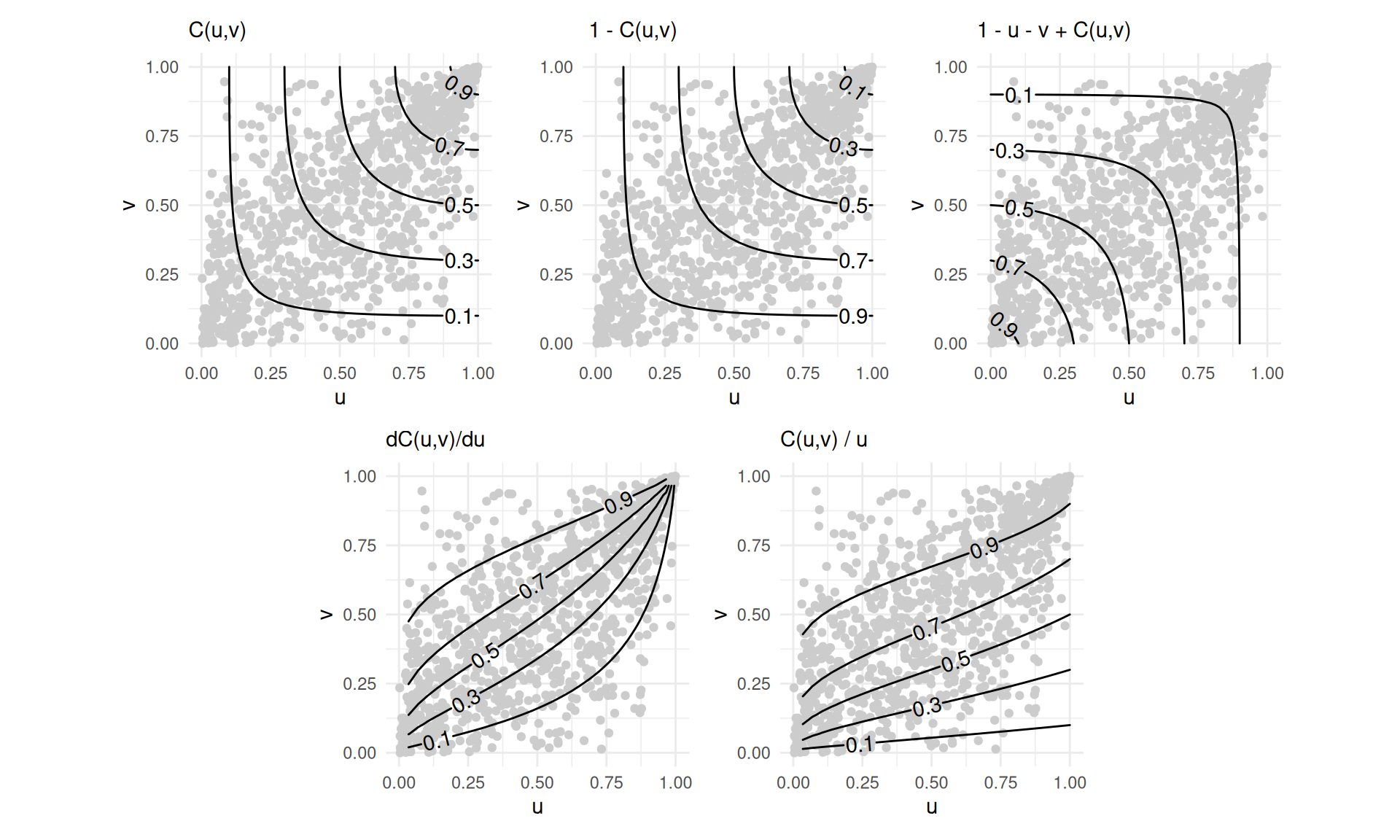
- Konkrétne je možné priamo odhadnúť pravdepodobnosti:
- \color{red}{Pr(U_1\leq u_1\wedge U_2\leq u_2)}=C(u_1,u_2), súčasného neprekročenia hodnôt u_1,u_2;
- Pr(U_1 > u_1\vee U_2 > u_2)=1-C(u_1,u_2), že aspoň jedna premenná prekročí daný prah;
- \color{blue}{Pr(U_1> u_1\wedge U_2> u_2)}=1-u_1-u_2+C(u_1,u_2), súčasného prekročenia (survival function);
- Pr(U_1\leq u_1 | U_2=u_2)=\frac{\partial C(u_1,u_2)}{\partial u_2}, neprekročenia pri jednej prem. za podmienky, že druhá dosiahla určitý prah,
- Pr(U_1\leq u_1 | U_2\leq u_2)=\frac{C(u_1,u_2)}{u_2}, prípadne. že ho neprekročila
- Pr(U_1>u_1 | U_2>u_2)=1-\frac{u_1-C(u_1,u_2)}{1-u_2}, resp. prekročila.
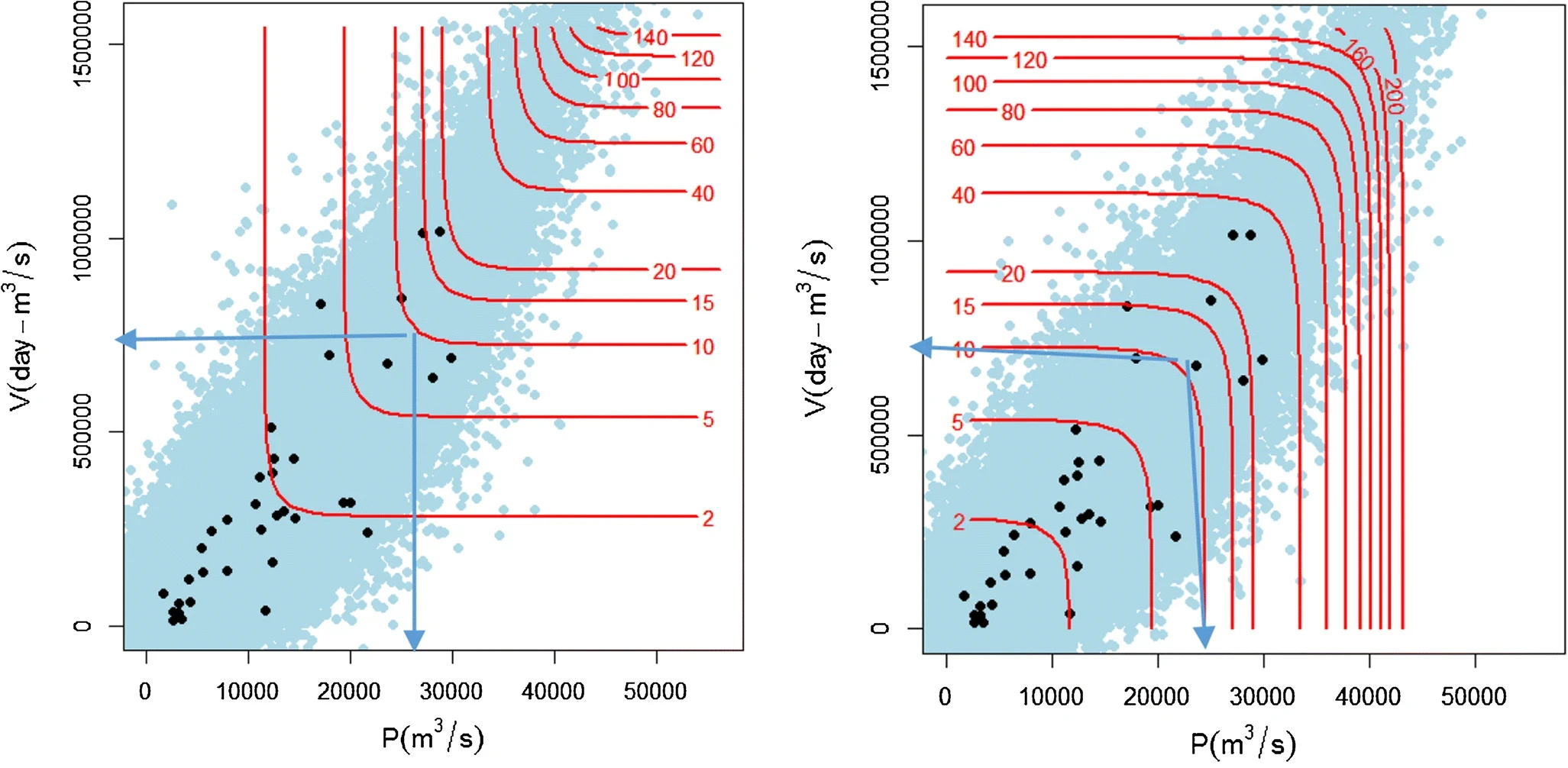
- V hydrologickej praxi sa často konštruuje vrstevnicový graf pravdepodobnostného rozdelenia na odčítanie doby návratu T=\frac{1}{\lambda\cdot Pr(X_1>x_1\quad{\color{blue}{\boldsymbol\wedge}}/{\color{green}{\boldsymbol\vee}}\quad X_2>x_2)}\text{ [čas.j.]} extrémneho javu (povodeň, zrážky, sucho), kde \lambda predstavuje priemerný počet extrémnych udalostí za danú časovú jednotku.
- Napr. doba návratu (v rokoch) povodňovej vlny charaktrizovanej objemom V (volume) a kulminačným prietokom P (peak) pre pravdepodobnosti súčasného (\color{blue}{vľavo}) alebo “jednotlivého” (\color{green}{vpravo}) prekročenia daných hodnôt veličín V a P. Graf obsahuje pozorované (čierne body) aj simulované povodne.
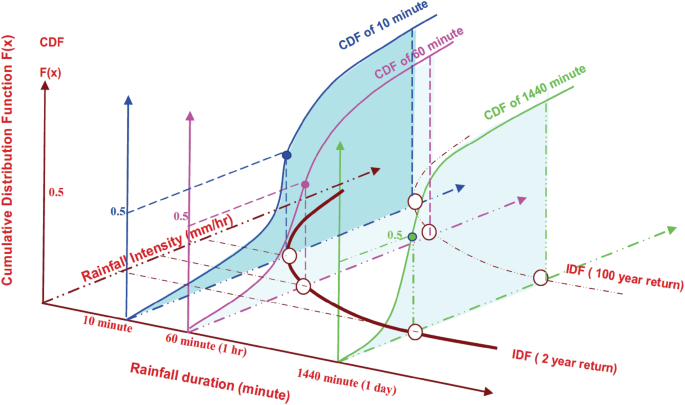
- Alebo doba návratu zrážkovej udalosti charakterizovanej intenzitou a trvaním (duration) pre pravdepodobnosti súčasného neprekročenia. Vrstevnice distribučnej funkcie CDF sa tu označujú ako čiary IDF (intensity-duration-frequency curves).
11.5 Parametrické triedy
Nasledujúce triedy kopúl sú užitočné v 2D problémoch:
- Eliptické - napr. normálna (Gaussovská) alebo t-kopula, modelujú iba lineárny vzťah, konštruujú sa štandardizáciou marginálií eliptických rozdelení, C_\Phi(u_1,...,u_p)= \Phi \left[ \Phi_1^{-1} (u_1), ..., \Phi_p^{-1} (u_p)\right]
- Archimedovské - konštruujú sa relatívne jednoducho, pomocou generátora f\colon[0,1]\searrow[0,\infty) a vzťahu
C(u_1,\ldots,u_p)=f^{(-1)}\Big(f(u_1)+\ldots+f(u_p)\Big)
ale sú permutačne symetrické (exchangeability), najznámejšie sú podtriedy
- Gumbelova, f(x) = (-\log x)^\theta, \ \theta\in[1,\infty),
- Claytonova, f(x) = (x^{-\theta}-1)/\theta, \ \theta\in[-1,\infty)-\{0\},
- Frankova, f(x) = -\log \frac{e^{-\theta x}-1}{e^{-\theta }-1}, \ \theta\in\mathbb{R}-\{0\}.
- Extreme-value - napr. Gumbelova, Galambosova, Hüsler-Reiss, modelujú maximálne hodnoty, konštruujú sa pomocou dependence funkcie \ell\colon[0,\infty)^p\to[0,\infty) alebo Pickandsovej depend.funkcie D\colon\Delta_{p-1}\to[1/p,1] (kde \Delta_{p-1} je jednotkový simplex) \begin{split} C(u_1,\ldots,u_p)&=\exp(-\ell(-\log u_1,\ldots,-\log u_p))\\ &=e^{ \left(\sum_{i=1}^p \log u_i\right)\ D\left(\frac{\log u_1}{\sum_{i=1}^p \log u_i},\dots, \frac{\log u_p}{\sum_{i=1}^p \log u_i}\right)} \end{split} Pre p>2 je pomerne komplikované hľadať dependence funkcie.
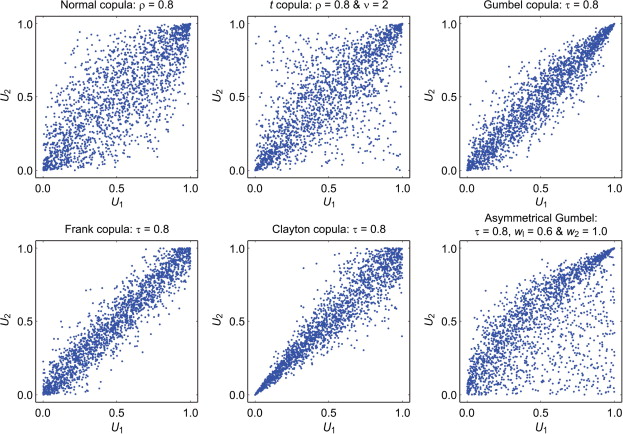
- Na obrázku šestice simulovaných náhodných výberov
- prvé dve sú z kopúl rozdelenia s eliptickými vrstevnicami,
- ďalšie tri Archimedovské (iba Frankova je radiálne symetrická),
- v poslednom stĺpci sú EV kopuly (líšia sa permutačnou symetriou).
Nasledujúce triedy (a konštrukčné metódy) sa v súčasnosti používajú ako dostatočne flexibilné a zároveň analyticky rozumne dostupné vo viacrozmerných problémoch:
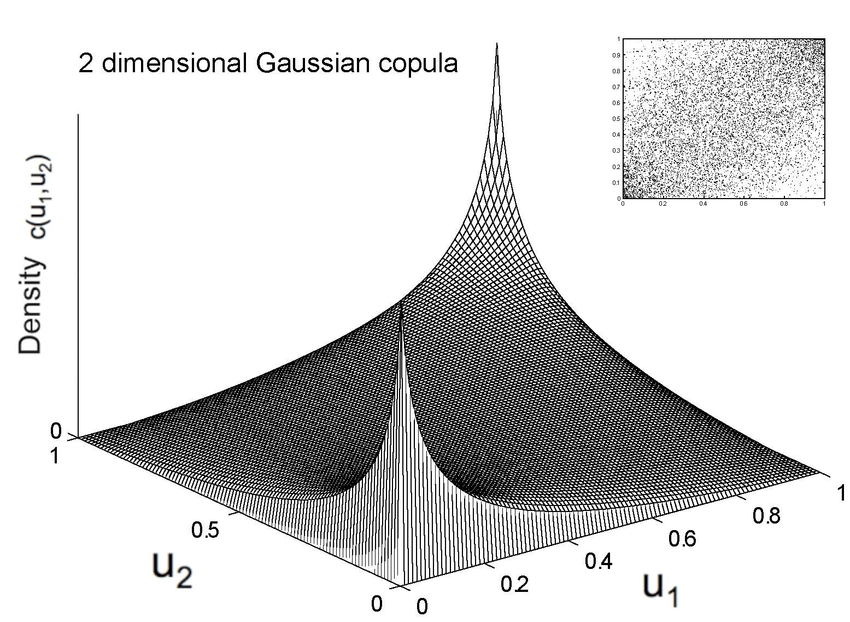
- Eliptické kopuly s explicitným vyjadrením hustoty, napr. Gaussovská kopula s korelačnou maticou \mathbf{R} a kvantilovou funkciou normovaného norm. rozd. \Phi^{-1}, c(\vec u)=\frac1{\sqrt{|\mathbf{R}|}}e^{-\frac12\Big(\Phi^{-1}(u_1),\ldots,\Phi^{-1}(u_p)\Big)(\mathbf{R}^T-\mathbf{I})\Big(\Phi^{-1}(u_1),\ldots,\Phi^{-1}(u_p)\Big)^T}
Hierarchické Archimedovské kopuly sú zložené z Archimedovských kopúl, napr. \begin{split} C(u_1,u_2,u_3) = \\ C_3\Big(C_2\big(C_1(u_1,u_2),u_3\big),u_4\Big) \qquad & \qquad C_3\Big(C_1(x_1,x_2),C_2(x_3,x_4)\Big)\\ \text{fully nested} \qquad & \qquad \text{partially nested} \end{split}
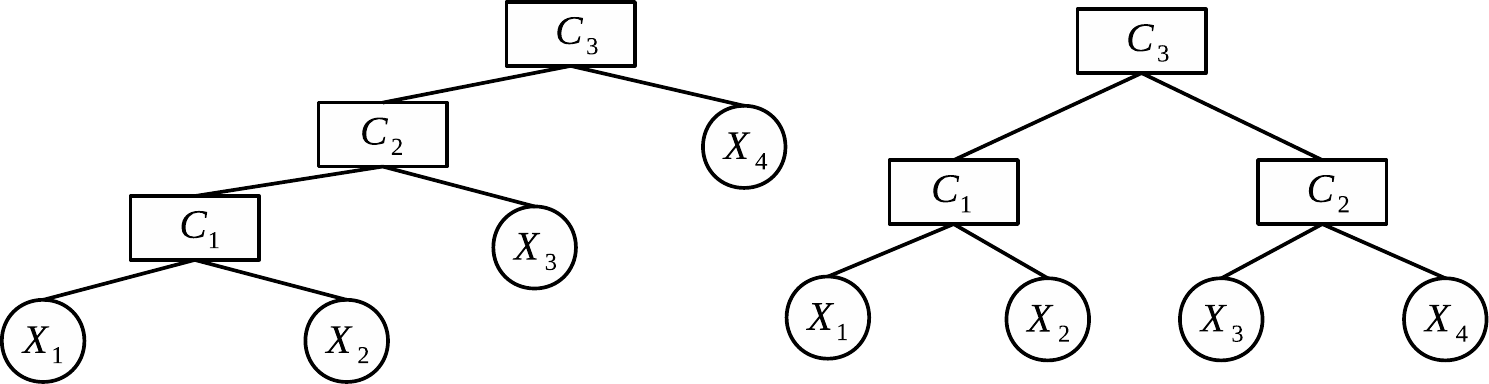
C_1,C_2,C_3 však musia byť z rovnakej parametrickej triedy (parametric family) Archimedovských kopúl a závislosť musí s úrovňou hierarchie klesať.
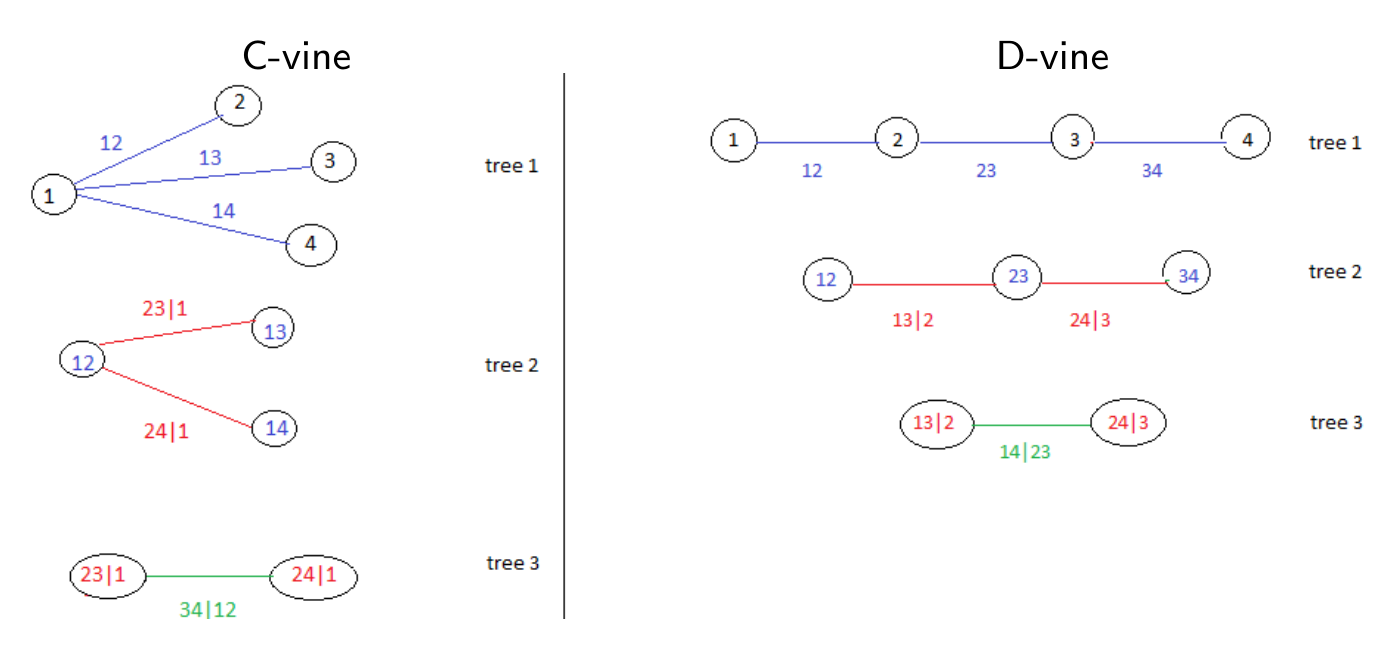
Vine kopuly využívajú podmienenú pravdepodobnosť na faktorizáciu viacrozmerného združeného rozdelenia pomocou dvojrozmerných kopúl (pair-copula decomposition).
- Napr. pre p=3 jeden z možných zápisov (rozkladov) je
\begin{split}
f(x_1,x_2,x_3) & = f_1(x_1) \cdot f_{2|1}(x_2|x_1) \cdot f_{3|12}(x_3|x_1,x_2) \\
&= f_1(x_1) \cdot \\
&\phantom{=} \cdot c_{12} \left[ F_1(x_1),F_2(x_2)\right] \cdot f_2(x_2) \cdot \\
&\phantom{=}
\cdot c_{31|2} \left[ F_{3|2}(x_3|x_2),F_{1|2}(x_1|x_2)\right] \cdot
\underbrace{c_{23} \left[ F_2(x_2),F_3(x_3)\right] \cdot f_3(x_3)}_{f_{3|2}(x_3|x_2)}
\end{split}
kde sme použili úpravu f_{2|1}(x_2|x_1)=\frac{f(x_1,x_2)}{f_1(x_1)}=\frac{c_{12}\big(F_1(x_1),F_2(x_2)\big)f_1(x_1)f_2(x_2)}{f_1(x_1)} (pričom podobne bola vyjadrená aj hustota f_{3|12}, kde sme z podmieňujúcich premenných zvolili X_2), a podmienené distribučné funkcie F_{i|j}(x_i|x_j)=\frac{\partial C_{ij}\big(F_i(x_i),F_j(x_j)\big)}{\partial F_j(x_j)}.
- S pribúdajúcimi rozmermi rastie aj komplexnosť všetkých možných rozkladov, preto je model graficky reprezentovaný sekvenciou vnorených stromov s neorientovanými hranami (vine tree).
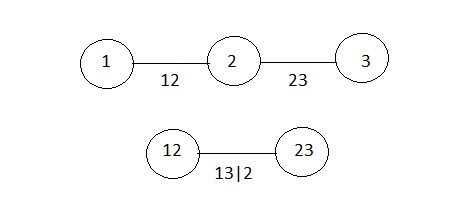
- Pri viac ako troch premenných môžu mať všeobecné vine stromy (regular vines) rôzne tvary, najpopulárnejšie sú C-vine (canonical) a D-vine (drawable).
- Napr. pre p=3 jeden z možných zápisov (rozkladov) je
\begin{split}
f(x_1,x_2,x_3) & = f_1(x_1) \cdot f_{2|1}(x_2|x_1) \cdot f_{3|12}(x_3|x_1,x_2) \\
&= f_1(x_1) \cdot \\
&\phantom{=} \cdot c_{12} \left[ F_1(x_1),F_2(x_2)\right] \cdot f_2(x_2) \cdot \\
&\phantom{=}
\cdot c_{31|2} \left[ F_{3|2}(x_3|x_2),F_{1|2}(x_1|x_2)\right] \cdot
\underbrace{c_{23} \left[ F_2(x_2),F_3(x_3)\right] \cdot f_3(x_3)}_{f_{3|2}(x_3|x_2)}
\end{split}
kde sme použili úpravu f_{2|1}(x_2|x_1)=\frac{f(x_1,x_2)}{f_1(x_1)}=\frac{c_{12}\big(F_1(x_1),F_2(x_2)\big)f_1(x_1)f_2(x_2)}{f_1(x_1)} (pričom podobne bola vyjadrená aj hustota f_{3|12}, kde sme z podmieňujúcich premenných zvolili X_2), a podmienené distribučné funkcie F_{i|j}(x_i|x_j)=\frac{\partial C_{ij}\big(F_i(x_i),F_j(x_j)\big)}{\partial F_j(x_j)}.
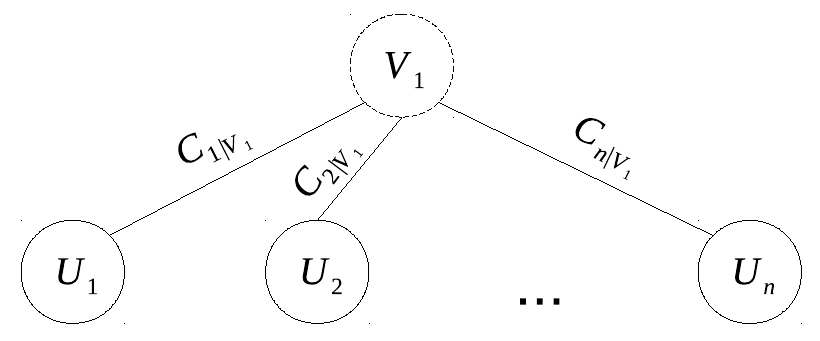
- Faktorové kopuly. V jednofaktorovom modeli je závislosť medzi premennými U_i indukovaná faktorom V_1 cez tzv. linking kopuly C_{i|V_1}, na ktoré nie sú kladené žiadne obmedzenia, C(u_1,\ldots,u_p)=\int_0^1\prod_{i=1}^p C_{i|V_1}(u_i,v_1)dv_1
11.6 Odhad parametrov rozdelenia
Na odhad rozdelenia zo zvolenej parametrickej triedy sa používajú hlavne tieto tri metódy:
- Metóda zovšeobecnených komomentov – využíva priamy funkčný vzťah medzi zovšeobecnenými ko-momentami rozdelenia (ktoré sa dajú odhadnúť z náhodného výberu) \mu_g = E[g(X_1,..,X_p)] (pre vhodnú funkciu g) a parametrami rozdelenia \theta. Výhoda je v jednoduchosti (rýchlosti výpočtu), nevýhoda zas v častej nedostupnosti takých vzťahov, a tiež v tom, že metóda nedosahuje vlastnosti optimálneho odhadu ako ostatné dve. Medzi zovšeobecnené komomenty patria okrem klasických momentov (stredná hodnota, rozptyl, …) a klasických komomentov (kovariancia, Pearsonov korelačný koeficient) aj miery monotónnej závislosti (Kendallovo tau, Spearmanovo rho, Blomqvistovo beta).
- Metóda maximálnej vierohodnosti (maximum likelihood, ML) - využíva hustotu rozdelenia na vyjadrenie pravdepodobnosti získania daných pozorovaní podmienenú danými parametrami, teda \hat\theta=\underset{\theta\in\Theta}{\arg\max}\frac1n\sum_{i=1}^n\ln f(X_{i1},\ldots,X_{ip}|\theta). Odhad je konzistentný (s rastúcim n pravdepodobnosťou konverguje k správnej hodnote), nevychýlený (angl. unbiased), výdatný (s najmenším rozptylom, angl. efficient) a normálne rozdelený (asymptoticky). Nevýhoda je v komplikovanosti výpočtu, vychýlenosti pre malé výbery a citlivosti na počiatočné podmienky.
- Metóda najmenších štvorcov - pomerne univerzálna metóda, hoci nemá tak dobré vlastnosti ako ML. Parametre môžu byť odhadnuté minimalizáciou napr. vzdialenosti teoretickej F a empirickej distribučnej funkcie \hat F_n, \hat\theta=\underset{\theta\in\Theta}{\arg\min}\sum_{i=1}^n\Big(F(X_{i1},\ldots,X_{ip}|\theta) - \hat F_n(X_{i1},\ldots,X_{ip})\Big)^2
V praxi sa odhad parametrov združeného rozdelenia často rozdelí na odhad parametrov marginálnych rozdelení a kopule.
Na odhad kopule sa používajú pseudo-pozorovania získané transformáciou pozorovaní pomocou empirickej distribučnej funkcie danej premennej (prakticky ide o poradia normované počtom pozorovaní). Je to preto, aby parametrický odhad marginálií neovplyvnil odhad kopule.
Ako štartovacie hodnoty parametrov v metóde maximálnej vierohodnosti sa s výhodou využívajú odhady z metódy ko-momentov.
11.7 Miery monotónnej závislosti
- Miera lineárnej závislosti (korelácie) bola predstavená v predošlej kapitole. Je ňou Pearsonov korelačný koeficient. Jeho nevýhodou je, že závisí od marginálnych rozdelení.
- Miery, ktoré závisia iba od kopule (čiže nie od marginálií), sú založené na poradí (rank). Medzi najznámejšie patria \begin{split} \rho_K &= 4\iint_{[0,1]^2} C(u,v)dC(u,v)-1 \qquad\text{(Kendallovo tau)} \\ \rho_S &= 12\iint_{[0,1]^2} \Big(C(u,v)-uv\Big)dudv \qquad\text{(Spearmanovo rho)} \\ \rho_B &= 4\ C\left(\frac12,\frac12\right) - 1 \qquad\text{(Blomqvistovo beta)} \end{split}
- Tieto vzťahy sa dajú využiť prostredníctvom inverzie na odhad kopule. Hodnoty parametra sa však zväčša musia počítať numericky, a iba v niektorých prípadoch sa dajú vyjadriť explicitne, v uzavretom tvare:
- Clayton copula \theta = 2\rho_K/(1-\rho_K),
- Gumbel-Hougaard θ = 1/(1-\rho_K) = 1/\log_2\left(2 - \log_2(1 + \rho_B)\right),
- Gauss (normal) \theta = \sin(\pi\rho_K/2) = \sin(\pi\rho_B/2) = 2\sin(\pi\rho_S/6)
- Odhad koeficientov konkordancie z pozorovaných údajov je zhrnutý v nasledujúcich vzťahoch,
\begin{split}
\rho_K &= \frac{n_C-n_D}{n(n-1)/2} = \frac{2}{n(n-1)}\sum_{i<j}\mathrm{sgn}(x_j-x_i)\ \mathrm{sgn}(y_j-y_i) \\
\rho_S &= \mathrm{corr}\Big(\mathrm{rank}(x_i),\mathrm{rank}(y_i)\Big) = 1 - \frac{6\sum_{i=1}^n (\mathrm{rank}(x_i) - \mathrm{rank}(y_i))^2}{n(n^2-1)} \\
\rho_B &= \frac1n \sum_{i=1}^n\mathrm{sgn}\Big((x_i - \tilde x)(y_i - \tilde y)\Big)
\end{split}
kde
- n_C (n_D) je počet konkordantných (diskordantných) párov,
- \mathrm{rank}(x) je poradie x v zodpovedajúcom vektore pozorovaní,
- \tilde x (\tilde y) je medián premennej X (Y),
- a znamienková funkcia je definovaná vzťahom \mathrm{sgn}(x) = \begin{cases} 1 & x>0 \\ 0 & x=0 \\ -1 & x<0 \end{cases}
- Označme s_{ij} = (x_j-x_i)(y_j-y_i). Potom body (x_i,y_i) a (x_j,y_j) sú
- konkordantné, ak s_{ij}>0,
- viazané (tied), ak s_{ij}=0,
- diskordantné, ak s_{ij}<0.
11.8 Príklad
11.9 Literatúra
Kopuly
- Nelsen, R. B. (2007). An introduction to copulas. Springer Science & Business Media.
- Okhrin, O., Ristig, A., & Xu, Y. F. (2017). Copulae in high dimensions: an introduction. Applied quantitative finance, 247-277.
- Joe, H. (2015). Dependence modeling with copulas. no. 134 in monographs on statistics and applied probability.
- Schirmacher, D., Schirmacher, E. (2008). Multivariate dependence modeling using pair-copulas. Technical report.
- Salvadori G., De Michele C. (2010) Multivariate multiparameter extreme value models and return periods: a copula approach. DOI