# Function to
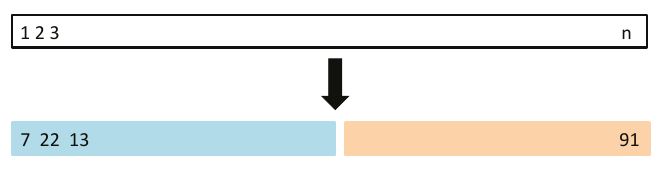
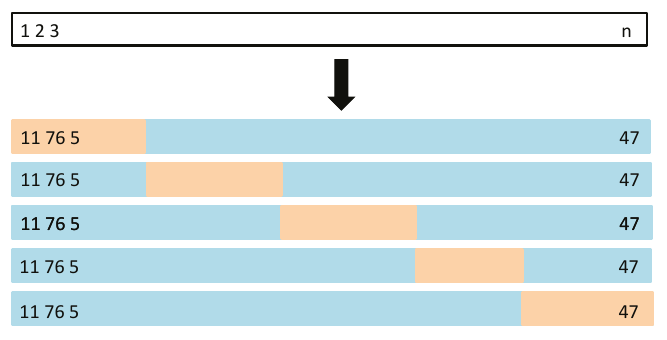
# 1. split the data proportionaly into training and evaluation sample,
# 2. fit the linear model given by formula to training set,
# 3. calculate MSE based on evaluation set.
# in: formula - formula defining relationship among variables,
# data - data frame to split
# proportion - numeric value in [0,1] interval, proportion of training sample to the whole set
# out: numeric value of MSE
mse_validset_lm <- function(formula, data, proportion = 1/2, seed = sample(1000,1)) {
n <- nrow(data)
set.seed(seed)
ind <- 1:n %in% sample(n, size = n*proportion)
train <- data[ind,]
valid <- data[!ind,]
fit <- lm(formula, train)
yname <- names(fit$model)[[1]]
RSS <- sum((valid[[yname]] - predict(fit, newdata = valid))^2)
df <- nrow(valid) - length(fit$coefficients)
RSS / df
}
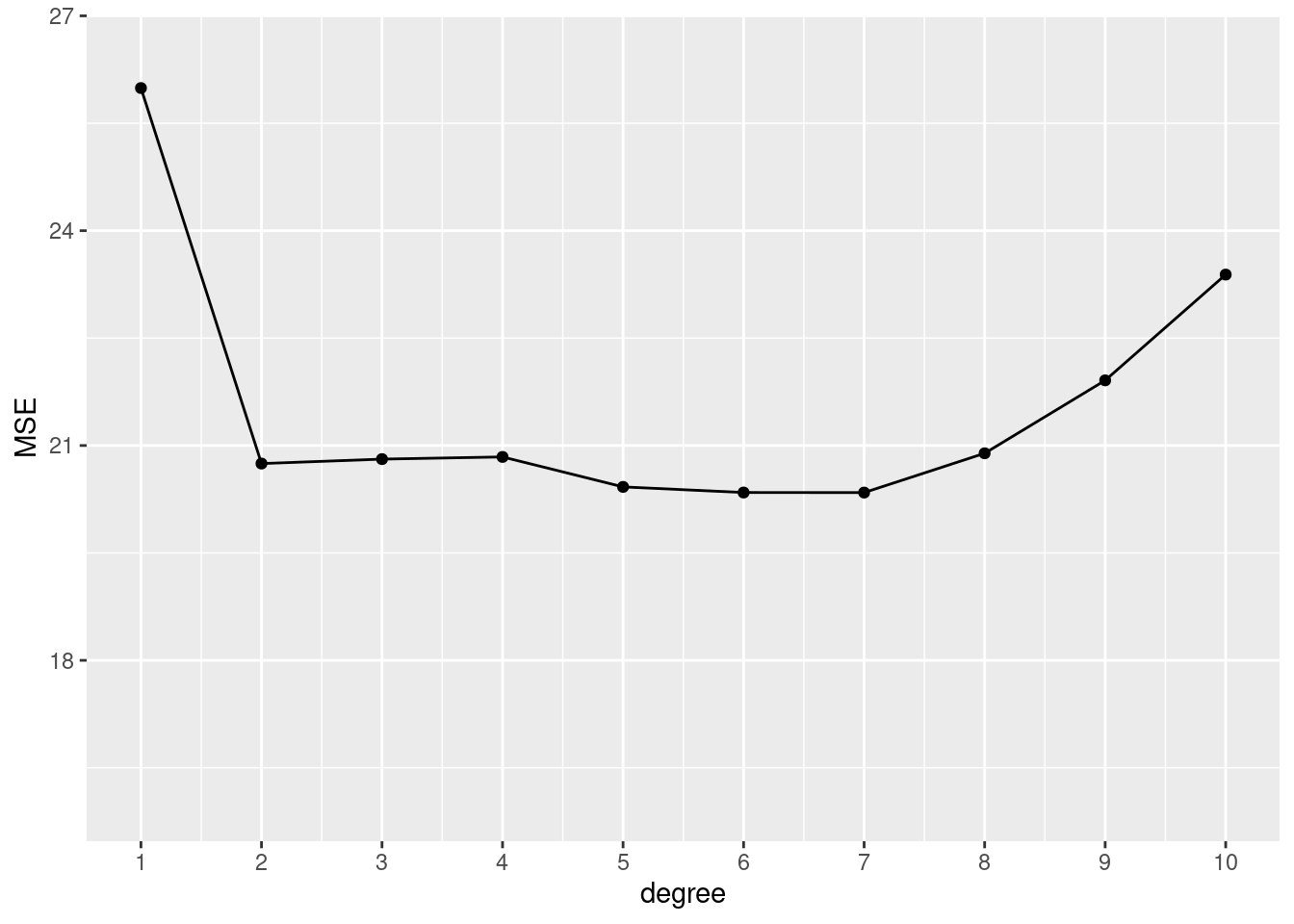
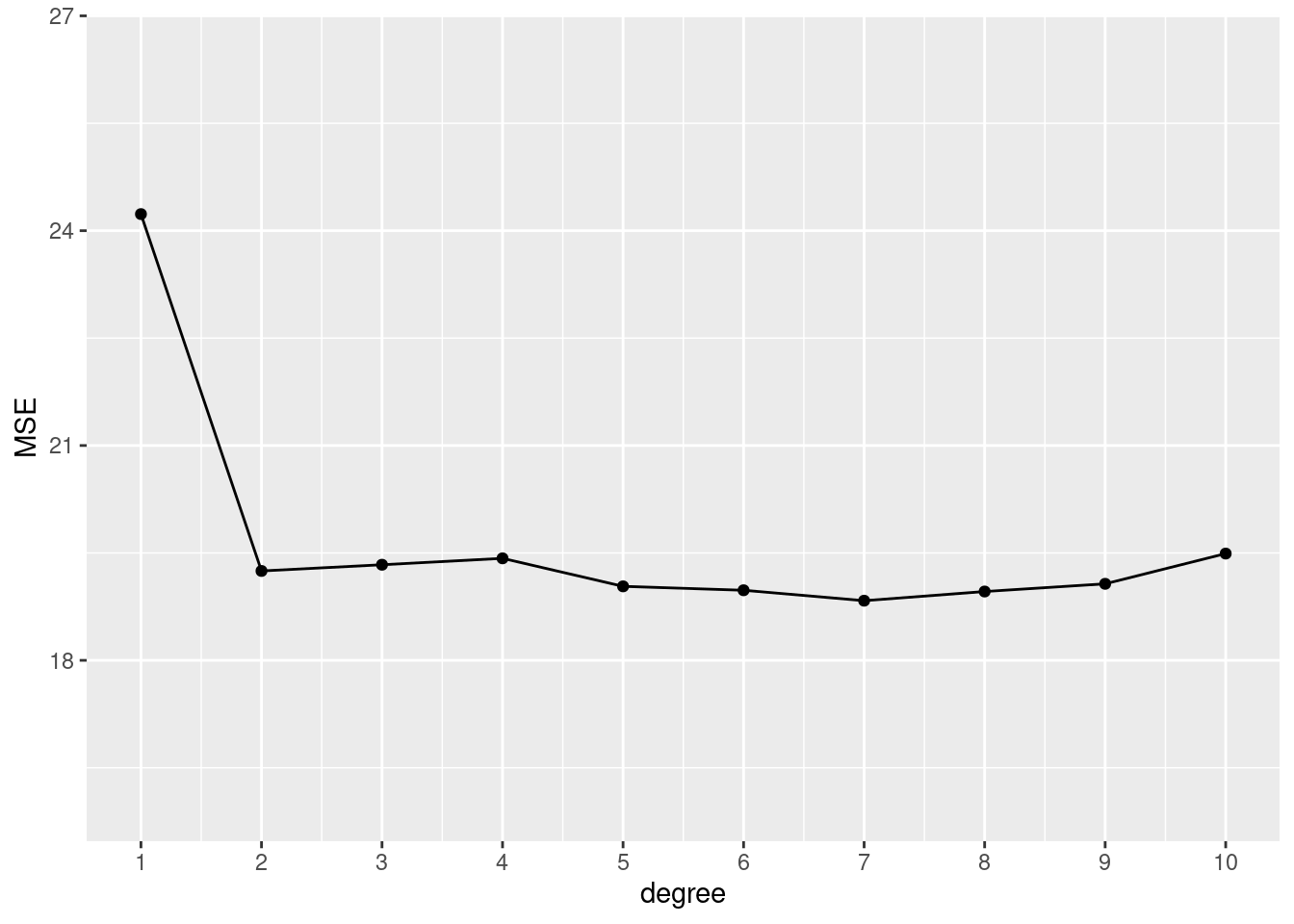
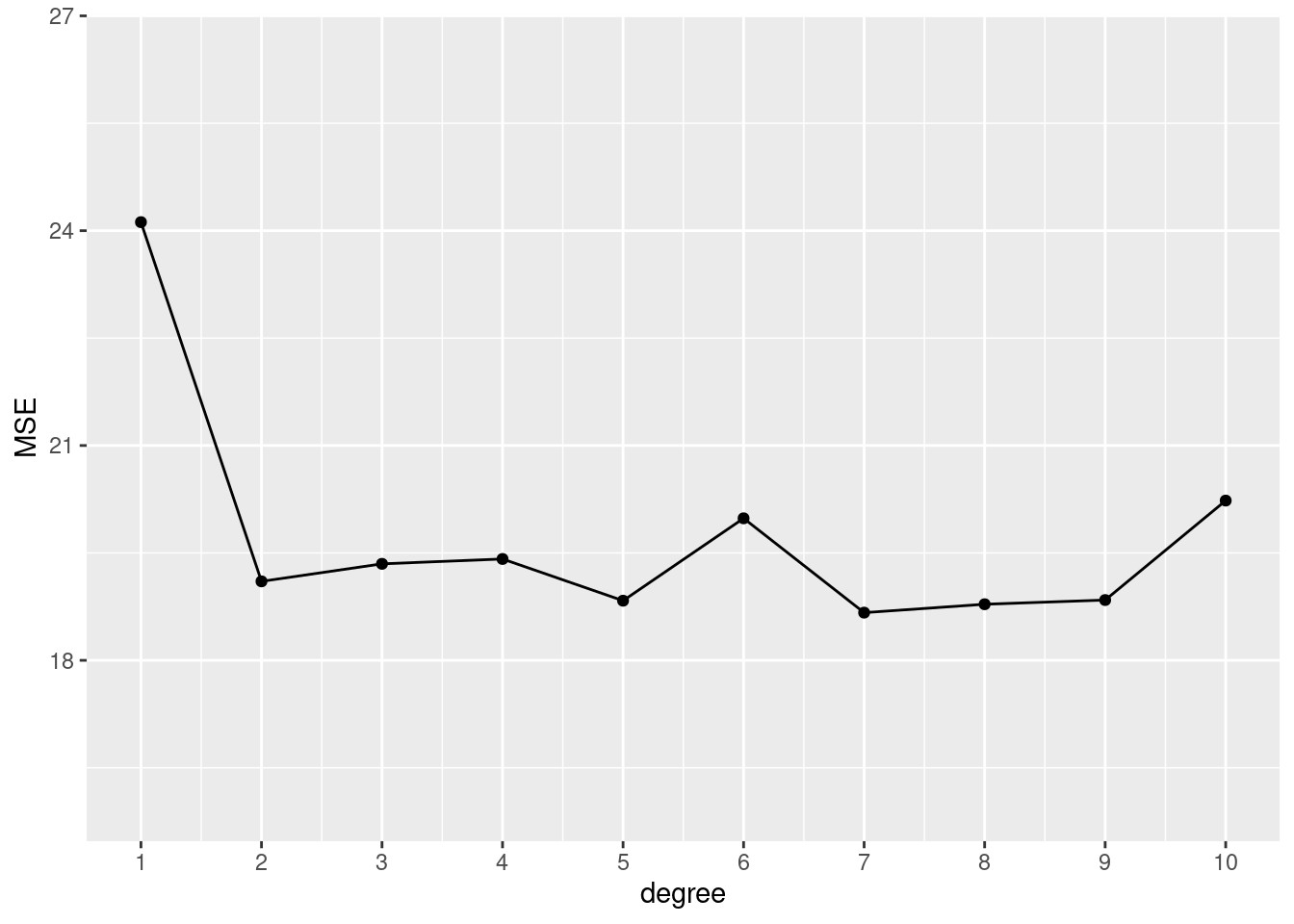
# 1 split, 10 polynomials of certain degrees
tibble::tibble(
degree = 1:10,
MSE = sapply(degree, function(x) mse_validset_lm(mpg ~ poly(horsepower, x),
ISLR2::Auto,
seed = 2))
) |>
ggplot() + aes(x = degree, y = MSE) +
geom_line() + geom_point() +
scale_x_continuous(n.breaks = 10) +
ylim(16, 26.5)
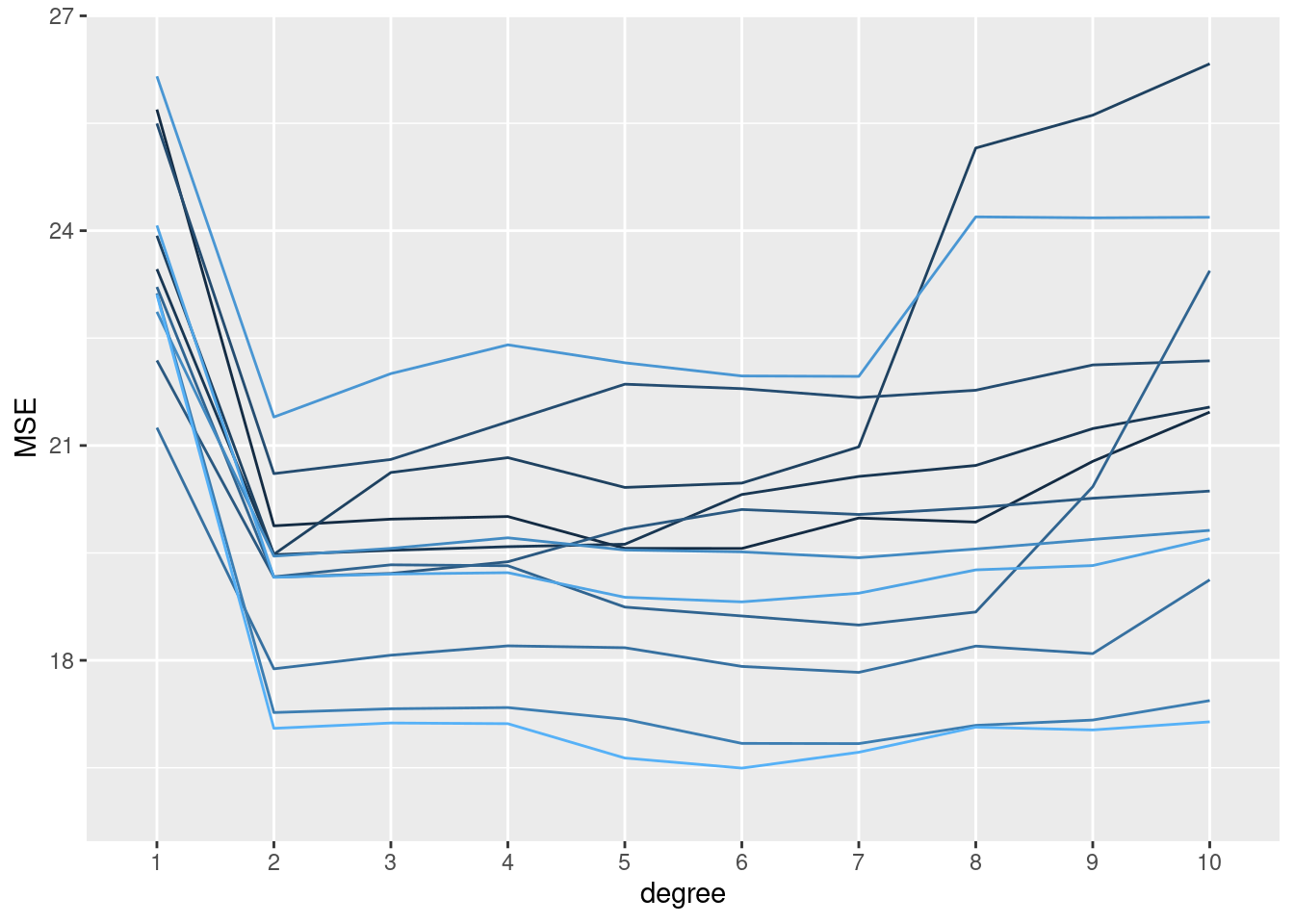
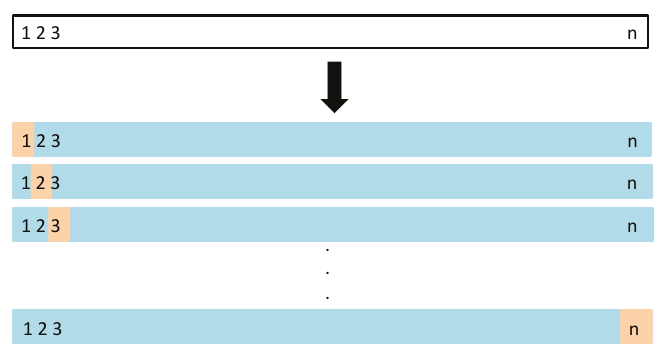
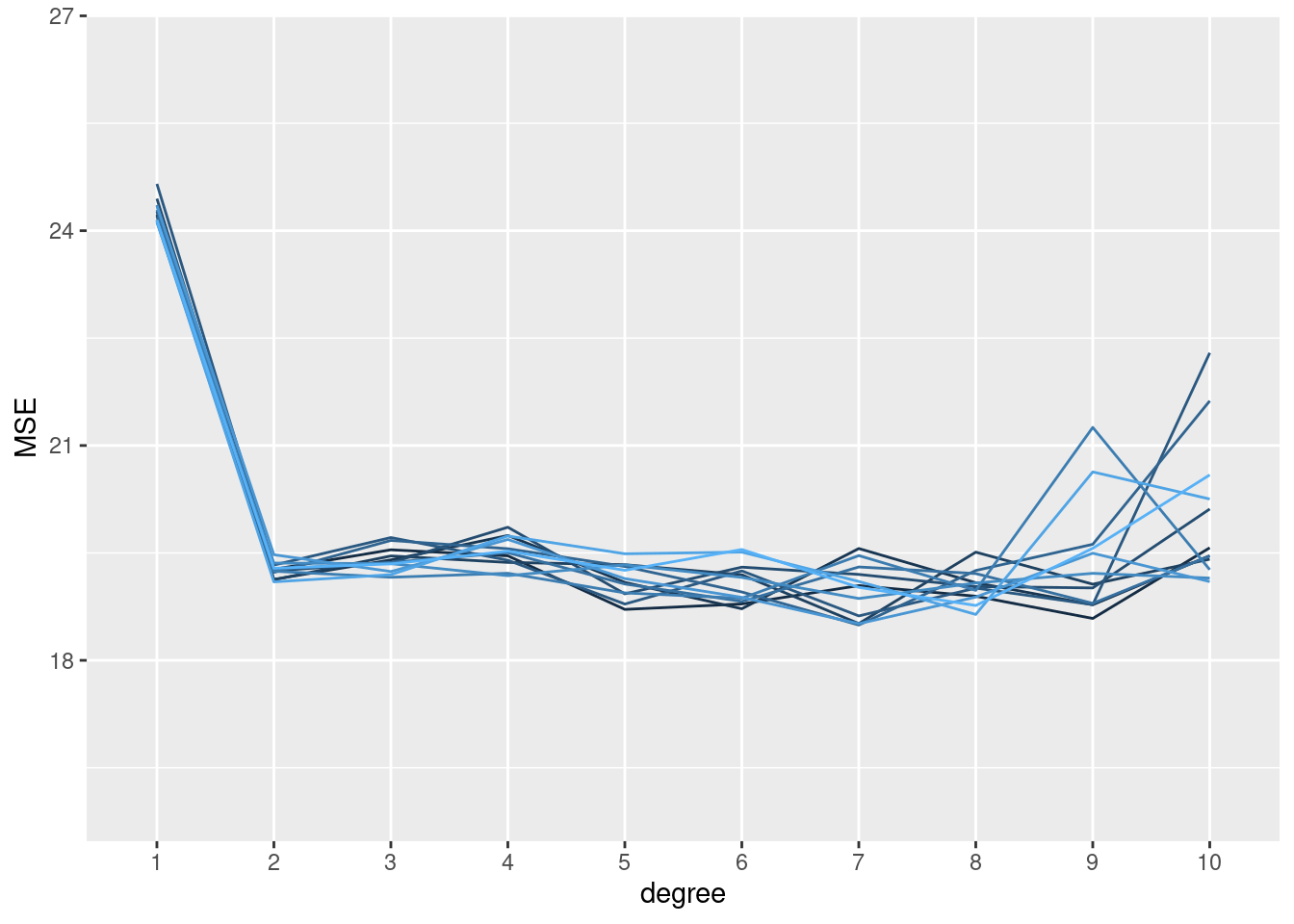
# 12 splits, 10 models
set.seed(1234)
replicate(n = 12, local({
seed <- sample(1000, 1)
sapply(1:10, function(x) mse_validset_lm(mpg ~ poly(horsepower, x),
ISLR2::Auto, seed = seed))
})
) |>
t() |> as.data.frame() |>
setNames(1:10) |>
dplyr::mutate(replication = 1:dplyr::n()) |>
tidyr::pivot_longer(-replication, names_to = "degree", values_to = "MSE",
names_transform = forcats::as_factor) |>
ggplot() + aes(x = degree, y = MSE, color = replication, group = replication) +
geom_line(show.legend = FALSE) +
ylim(16, 26.5)
# (General version)
# Function that for every observation from data repeats the following steps
# 1. fit the linear model given by formula to training set,
# where the one particular observation is ommited,
# 2. calculate MSE based on prediction for the ommited observation,
# and calculates average MSE.
# in: formula - formula defining relationship among variables,
# data - data frame of observations
# out: numeric value of MSE
mse_loocv_lm <- function(formula, data) {
n <- nrow(data)
y <- formula |> _[[2]] |> as.character() |> getElement(data, name = _)
df <- formula |> terms() |> attr("term.labels") |> length() |> (`+`)(1)
MSE <- sapply(1:n, function(i) {
lm(formula, data[-i,]) |>
predict(newdata = data[i,]) |>
(`-`)(y[i]) |>
(`^`)(2)
})
mean(MSE)
}
# (Effective version)
# Function, that implements the effective version of LOOCV, valid for linear models.
mse_loocv_lm <- function(formula, data) {
n <- nrow(data)
fit <- lm(formula, data)
eps <- residuals(fit)
h <- hatvalues(fit)
mean((eps/(1-h))^2)
}
# repeat for 10 models
# system.time(
dat_mse <- tibble::tibble(
degree = 1:10,
MSE = sapply(degree, function(x) mse_loocv_lm(mpg ~ poly(horsepower, x),
ISLR2::Auto))
)
# ) |> _["elapsed"] |> round(1) |> cat("time: ", a = _, "s")
# display
dat_mse |>
ggplot() + aes(x = degree, y = MSE) +
geom_line() + geom_point() +
scale_x_continuous(n.breaks = 10) + ylim(16, 26.5)
# built-in implementation of the general version:
# glm(mpg ~ poly(horsepower, 1), data = ISLR2::Auto) |>
# boot::cv.glm(data = ISLR2::Auto) |>
# _$delta[1]
# Function that uses boot::cv.glm to split observations into K folds and repeats the following steps
# 1. fit the linear model given by formula to training set,
# where one particular fold is ommited,
# 2. calculate MSE based on predictions for the ommited fold,
# and calculates average MSE.
# in: formula - formula defining relationship among variables,
# data - data frame of observations
# K - integer, number of folds
# out: numeric value of average MSE
mse_kfold_lm <- function(formula, data, K = 5) {
glm(formula, data = data) |> boot::cv.glm(data = data, K = K) |> _$delta[1]
}
# single run
set.seed(1)
tibble::tibble(
degree = 1:10,
MSE = sapply(degree, function(x)
mse_kfold_lm(mpg ~ poly(horsepower, x), data = ISLR2::Auto)
)
) |>
ggplot() + aes(x = degree, y = MSE) +
geom_line() + geom_point() +
scale_x_continuous(n.breaks = 10) + ylim(16, 26.5)
# 12-times repeat
replicate(n = 12, sapply(1:10, function(x)
mse_kfold_lm(mpg ~ poly(horsepower, x), ISLR2::Auto)
)) |>
t() |> as.data.frame() |>
setNames(1:10) |>
dplyr::mutate(replication = 1:dplyr::n()) |>
tidyr::pivot_longer(-replication, names_to = "degree", values_to = "MSE",
names_transform = forcats::as_factor) |>
ggplot() + aes(x = degree, y = MSE, color = replication, group = replication) +
geom_line(show.legend = FALSE) +
ylim(16, 26.5)
The Baron had fallen to the bottom of a deep lake. Just when it looked like all was lost, he thought to pick himself up by his own bootstraps.
Nasledujúci obrázok ilustruje bootstrap metódu pre n=3.
n <- 100
# Distribution of alpha based on samples from true population
# ----------------------------------------------
# number of data points and data sets
N <- 1000
# Function to construct bivariate covariance matrix from standard deviation 'sd' and correlation coefficient 'cor'.
make_cov_matrix <- function(sd = c(1,sqrt(1.25)), cor = 0.5/prod(sd)) {
diag(sd) %*% cbind(c(1,cor), c(cor,1)) %*% diag(sd)
}
# Function to calculate ratio alpha from bivariate covariance matrix.
make_alpha <- function(cov) {
(cov[2,2] - cov[1,2]) / (cov[1,1] + cov[2,2] - 2*cov[1,2])
}
# Function to generaten pairs from 2D normal distribution with mean vector 'mu' and covariance matrix 'cov'.
simulate_data <- function(n, mu = c(0,0), cov = make_cov_matrix()) {
X1 <- rnorm(n)
X2 <- rnorm(n)
cor <- cov[1,2]/sqrt(cov[1,1]*cov[2,2])
X3 <- cor * X1 + sqrt(1-cor^2) * X2
data.frame(X = mu[1] + sqrt(cov[1,1]) * X1,
Y = mu[2] + sqrt(cov[2,2]) * X3)
# alternatively: mvtnorm::rmvnorm(n, mu = mu, sigma = cov)
}
# simulate values of alpha
sim_alpha <- make_cov_matrix() |> # theoretical covariance
simulate_data(n = n, cov = _) |> # generate random data
cov() |> # estimate covariance
make_alpha() |> # calculate alpha
replicate(n = N) # repeat
# display hsitogram with true value of alpha indicated
sim_alpha |>
data.frame(alpha = _) |>
ggplot() + aes(x = alpha) +
geom_histogram(bins = 20, color = "white") +
geom_vline(xintercept = make_cov_matrix() |> make_alpha(),
color = 2, linewidth = 1) +
ggtitle("Simulation")
# Distribution of alpha based on bootstrap samples
# ----------------------------------------------
B <- 1000
# single data set of observations
set.seed(1)
dat <- simulate_data(n = 100)
# Function to make 'n' random drawings from 'data'.
resample_data <- function(data, n) {
ind <- sample(nrow(data), size = n, replace = TRUE)
data[ind,]
}
# make sampling distribution of alpha
boot_alpha <- dat |>
resample_data(n = 100) |>
cov() |>
make_alpha() |>
replicate(n = B)
# show sampling distribution of alpha
boot_alpha |>
data.frame(alpha = _) |>
ggplot() + aes(x = alpha) +
geom_histogram(bins = 20, color = "white") +
geom_vline(xintercept = make_cov_matrix() |> make_alpha(),
color = 2, linewidth = 1) +
geom_vline(xintercept = dat |> cov() |> make_alpha(),
color = 4, linewidth = 1) +
ggtitle("Bootstrap")
rbind(alpha = c(true = make_cov_matrix() |> make_alpha(),
sim = mean(sim_alpha),
boot = mean(boot_alpha)),
SE = c(true = NA,
sim = sd(sim_alpha),
boot = sd(boot_alpha))
) |> round(3) true sim boot
alpha 0.6 0.602 0.639
SE NA 0.081 0.071