Kód
plotly::plot_ly(USArrests,
x = ~Murder, y = ~Assault, z = ~Rape,
color = ~UrbanPop,
size = 2) |>
plotly::add_markers()
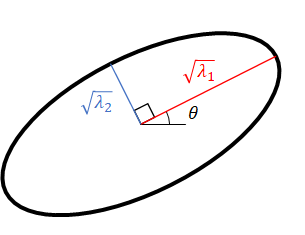
\mathbf{V} = \begin{pmatrix} \cos\theta & -\sin\theta \\ \sin\theta & \cos\theta \end{pmatrix}
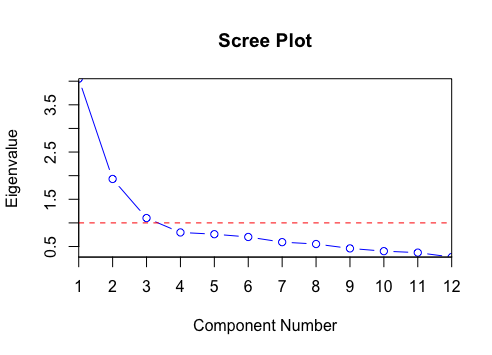
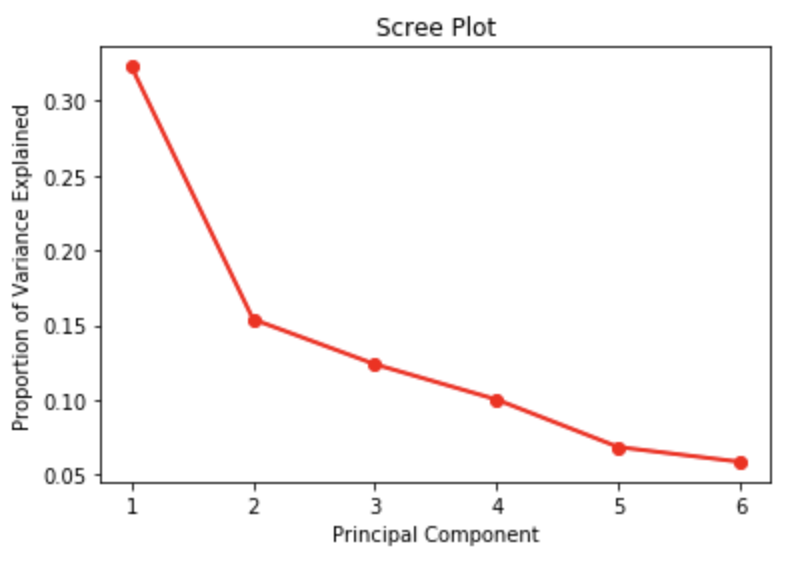
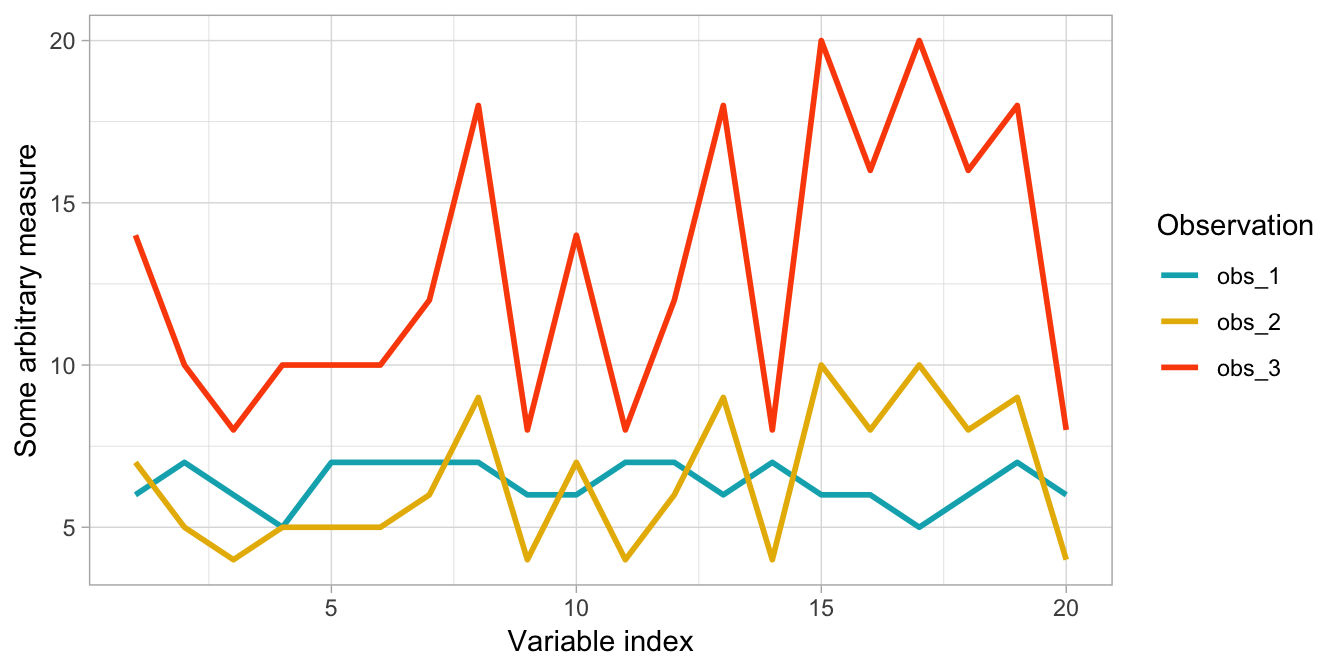
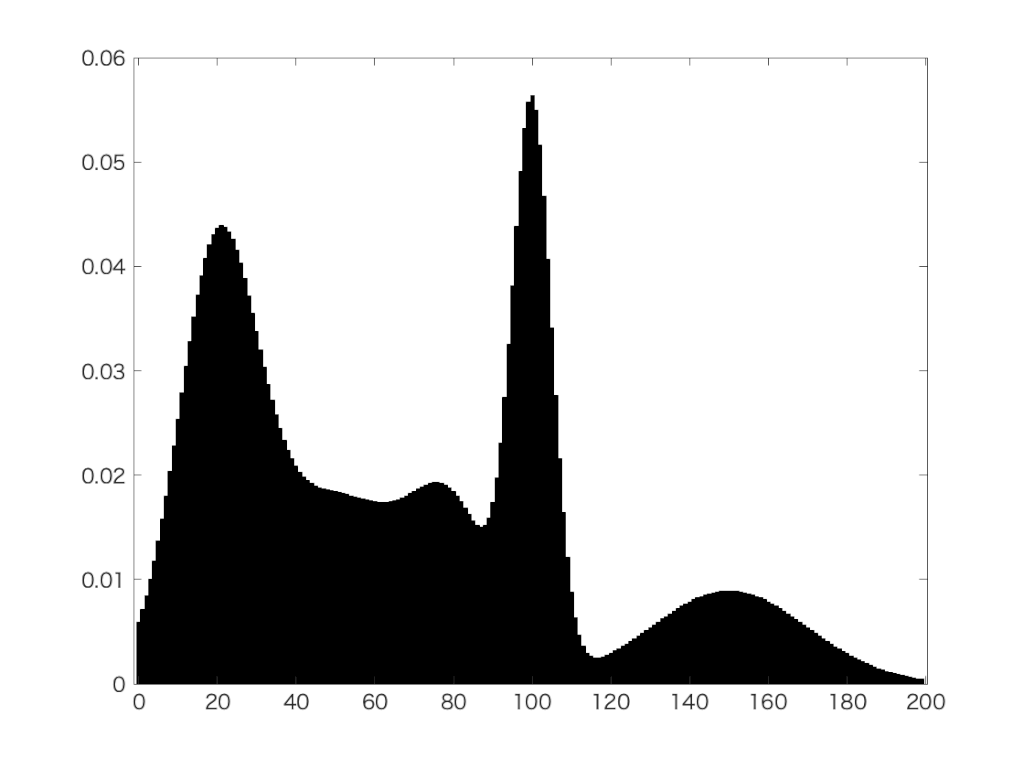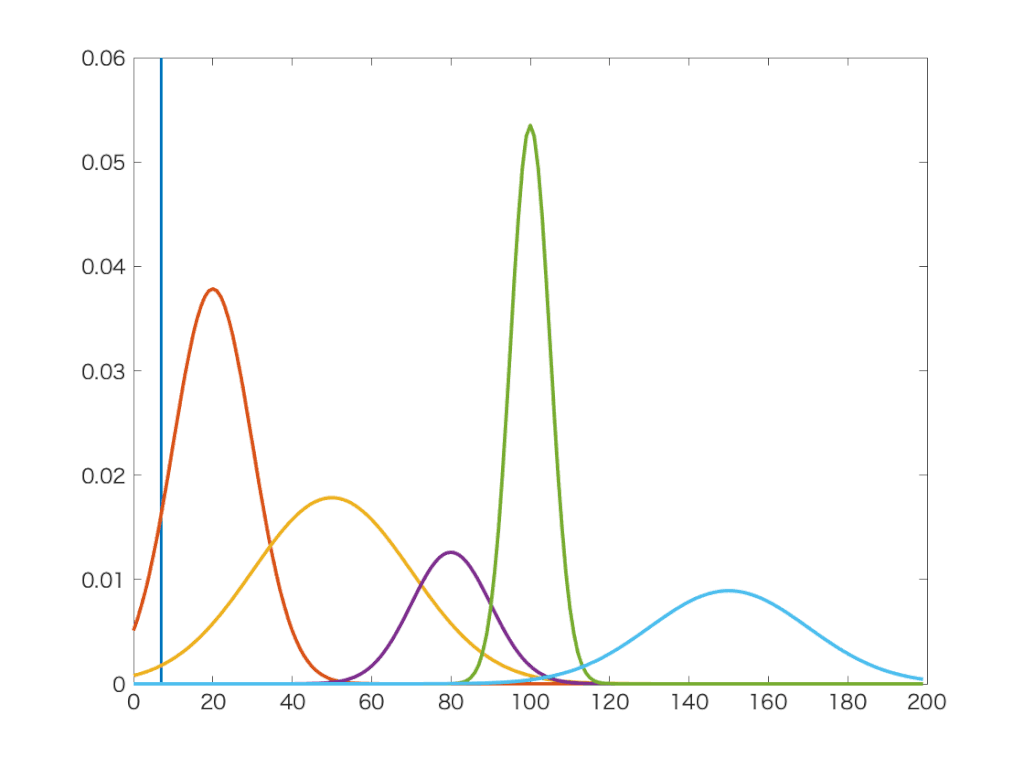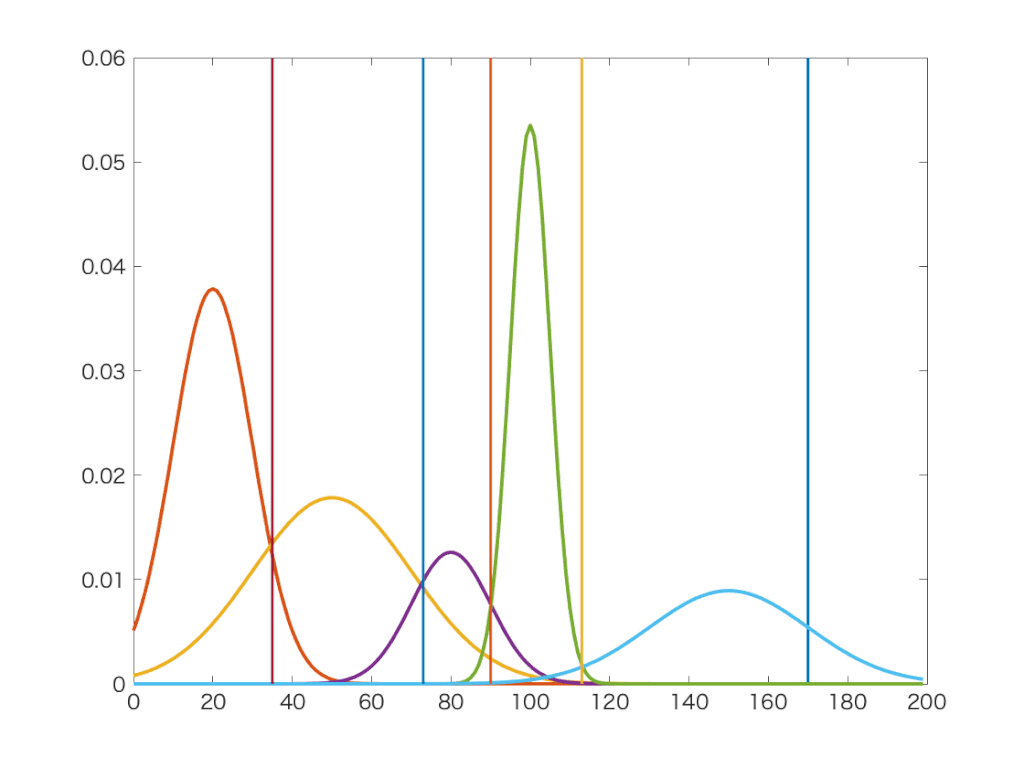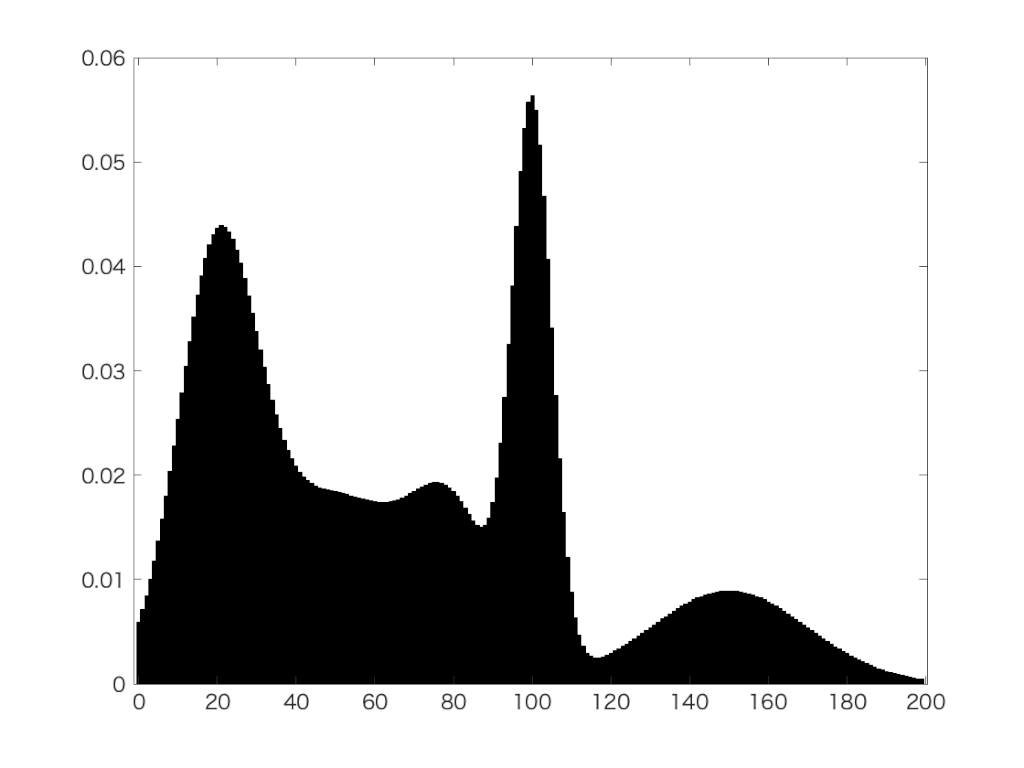
Jednoduchá a elegantná metóda.
Počet tried K treba definovať vopred.
Matematicky je problém formulovaný nasledovne: ak C_1,\ldots,C_K označujú množiny indexov objektov (pozorovaní) v každom zhluku, pričom
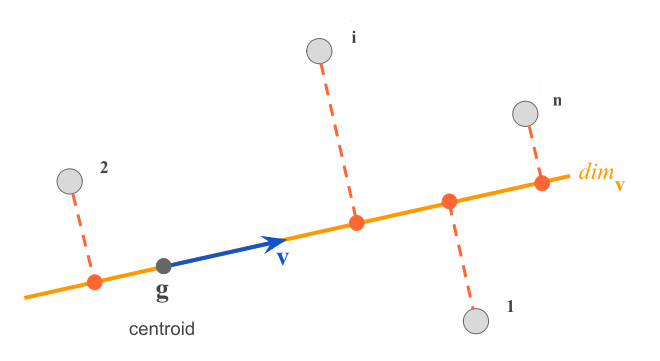
čiže každý objekt patrí práve do jedného zhluku, potom cieľom je minimalizovať vnútro-zhlukový rozptyl W, \underset{C_1,\ldots,C_K}{minimize}\left\{\sum_{k=1}^K W(C_k)\right\},\qquad\text{kde}\quad W(C_k)=\frac1{n_k}\sum_{i\in C_k}\sum_{j=1}^p(x_{ij}-g_{kj})^2, g_{kj}=\frac1{n_k}\sum_{i\in C_k}x_{ij} a použitá bola euklidovská vzdialenosť.
Nájsť presné riešenie je veľmi náročné.
Našťastie existuje jednoduchý algoritmus, ktorým sa dá nájsť celkom dobré riešenie, aj keď predstavuje iba lokálne optimum.
S danými počiatočnými hodnotami centroidov \mathbf{g}_1,\ldots,\mathbf{g}_K sa opakujú nasledujúce kroky:
až kým sa zaradenie v bode 1 nezmení.
Počiatočné hodnoty sa určia buď
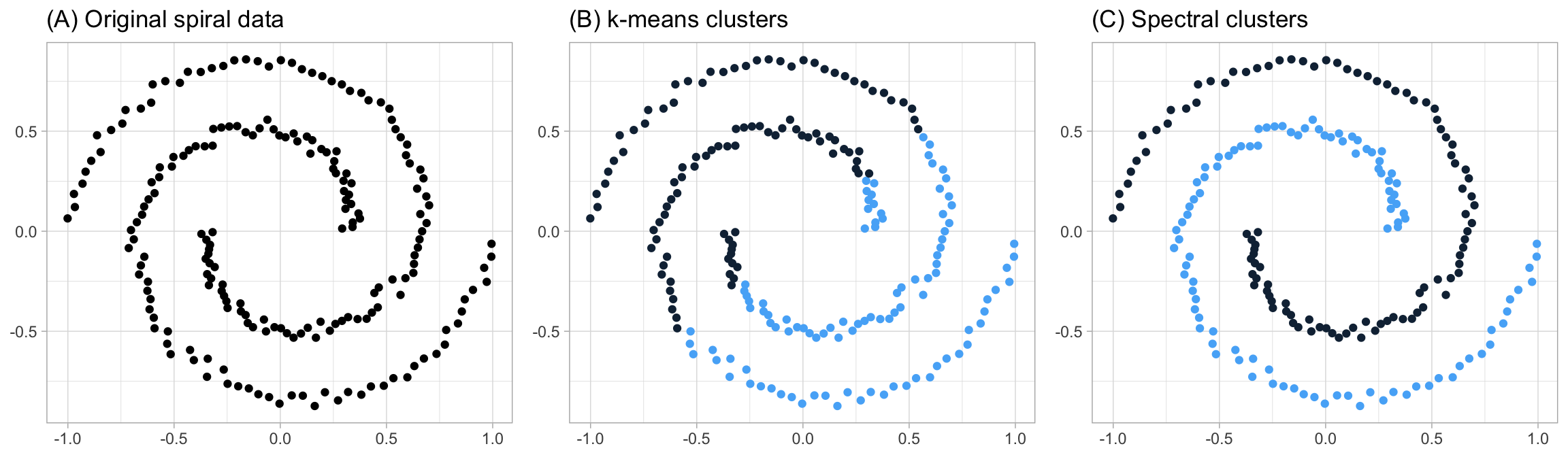
dat1 <- data.frame(
X1 = c(-1.5, -1.4, -1.0, -0.6, -0.1, 0.1, 0.7, 1.3, 1.5),
X2 = c(-0.4, -1.5, -1.1, -1.0, 0.9, -0.8, -0.2, -0.3, 0.0)
)
plot(X2 ~ X1, dat1, asp = 1, type = "n")
text(X2 ~ X1, dat1, labels = row.names(dat1))
fit <- dat1 |>
dist() |> # distance matrix calculation
hclust() # hierarchical clustering
plot(fit, ann = FALSE)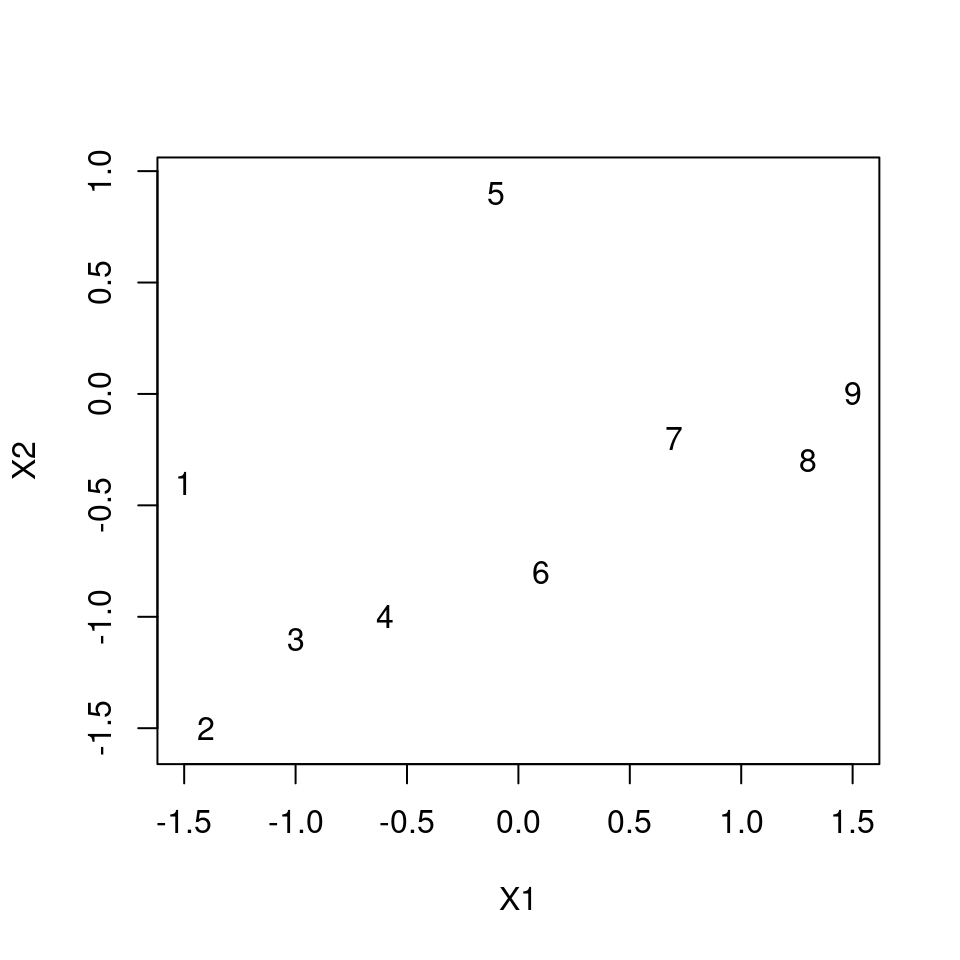
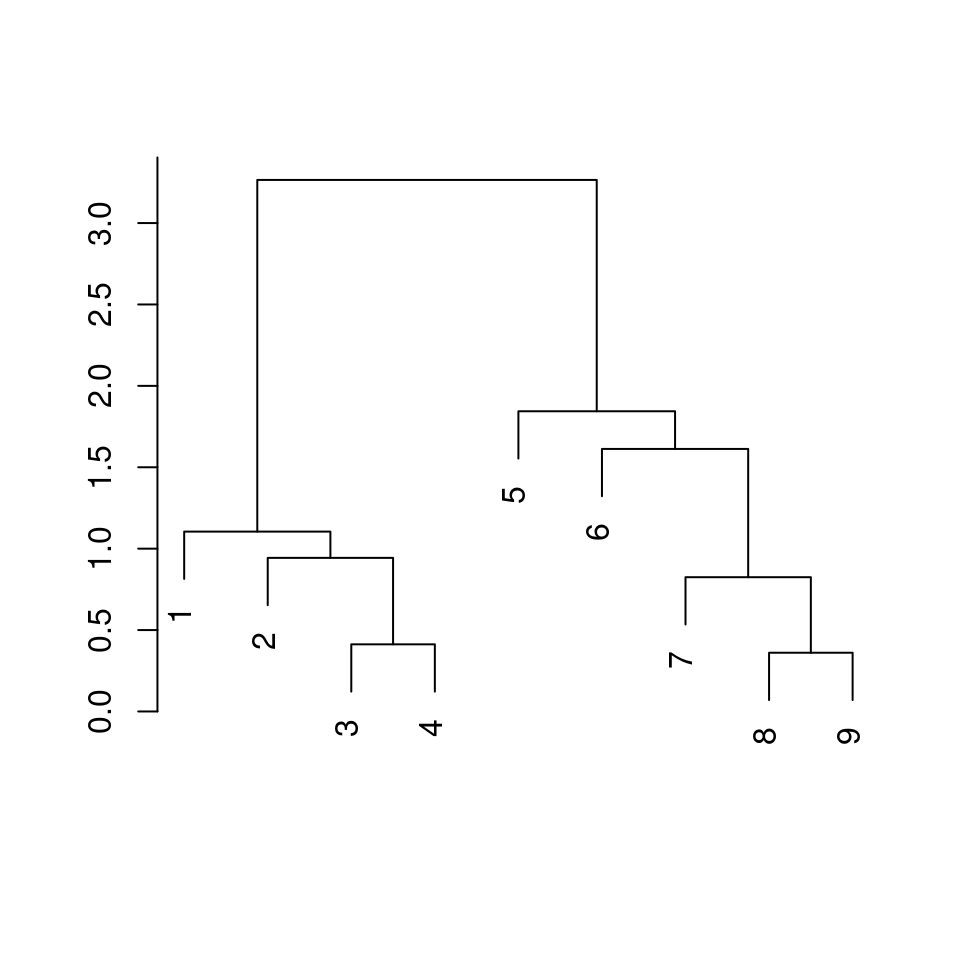
# generate data
set.seed(1)
dat <- list(A = c(-5,0), B = c(0,0), C = c(1,3)) |>
lapply(mvtnorm::rmvnorm, n = 15, sigma = diag(2)) |>
lapply(as.data.frame) |>
lapply(setNames, nm = paste0("X",1:2)) |>
dplyr::bind_rows(.id = "class") |>
dplyr::mutate(class = as.factor(class))
# fit model
fit <- dat |>
dplyr::select(-class) |>
dist() |>
hclust()
# --- visualize result
# basic dendrogram
#fit |>
# plot(hang = -1, cex = 0.6, main="", ylab="")
# cut to get 2 clusters
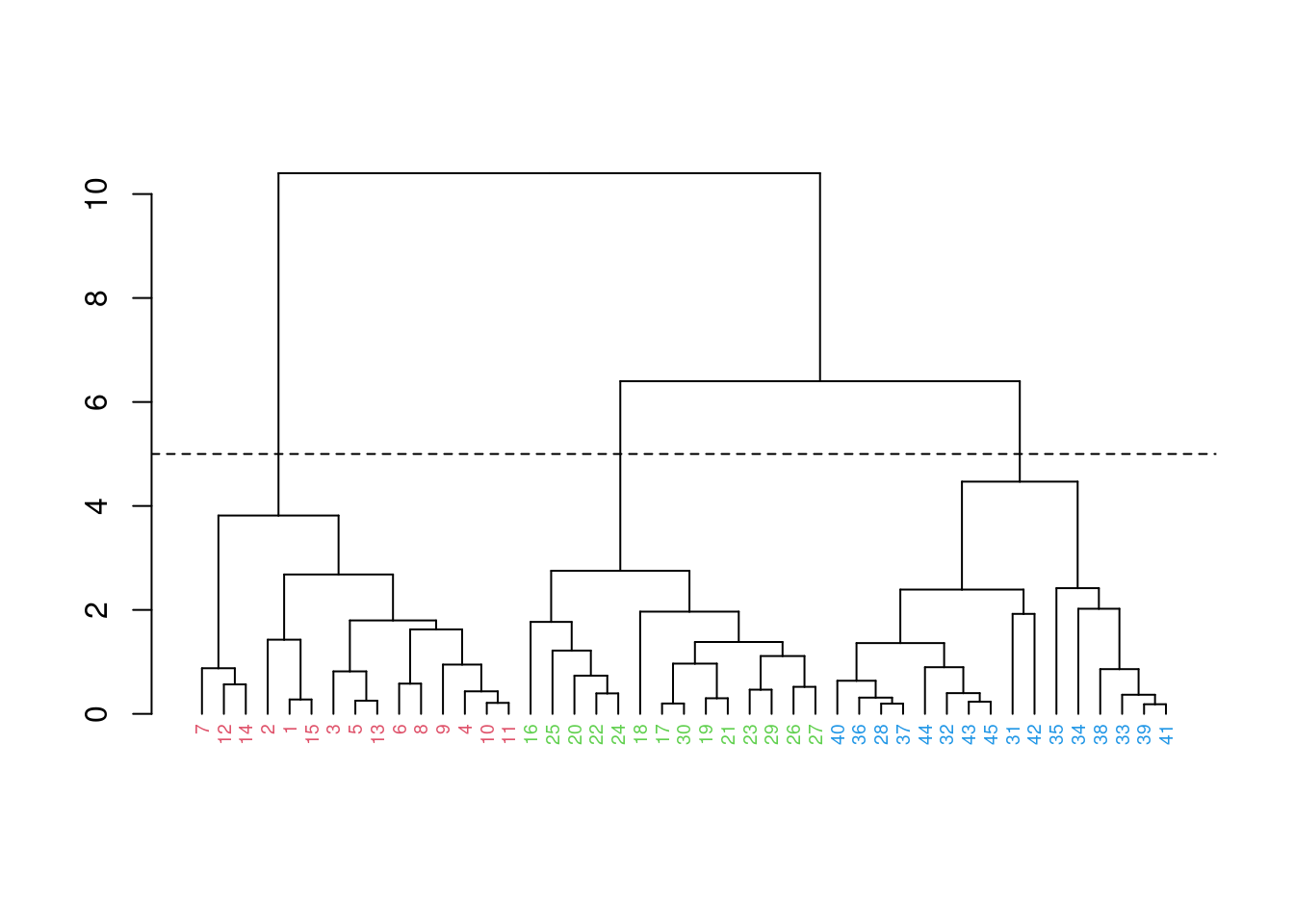
fit |>
as.dendrogram() |>
dendextend::set("labels_col", 2:3, k=2) |>
dendextend::set("labels_cex", 0.6) |>
plot()
abline(h = 8, lty = 2)
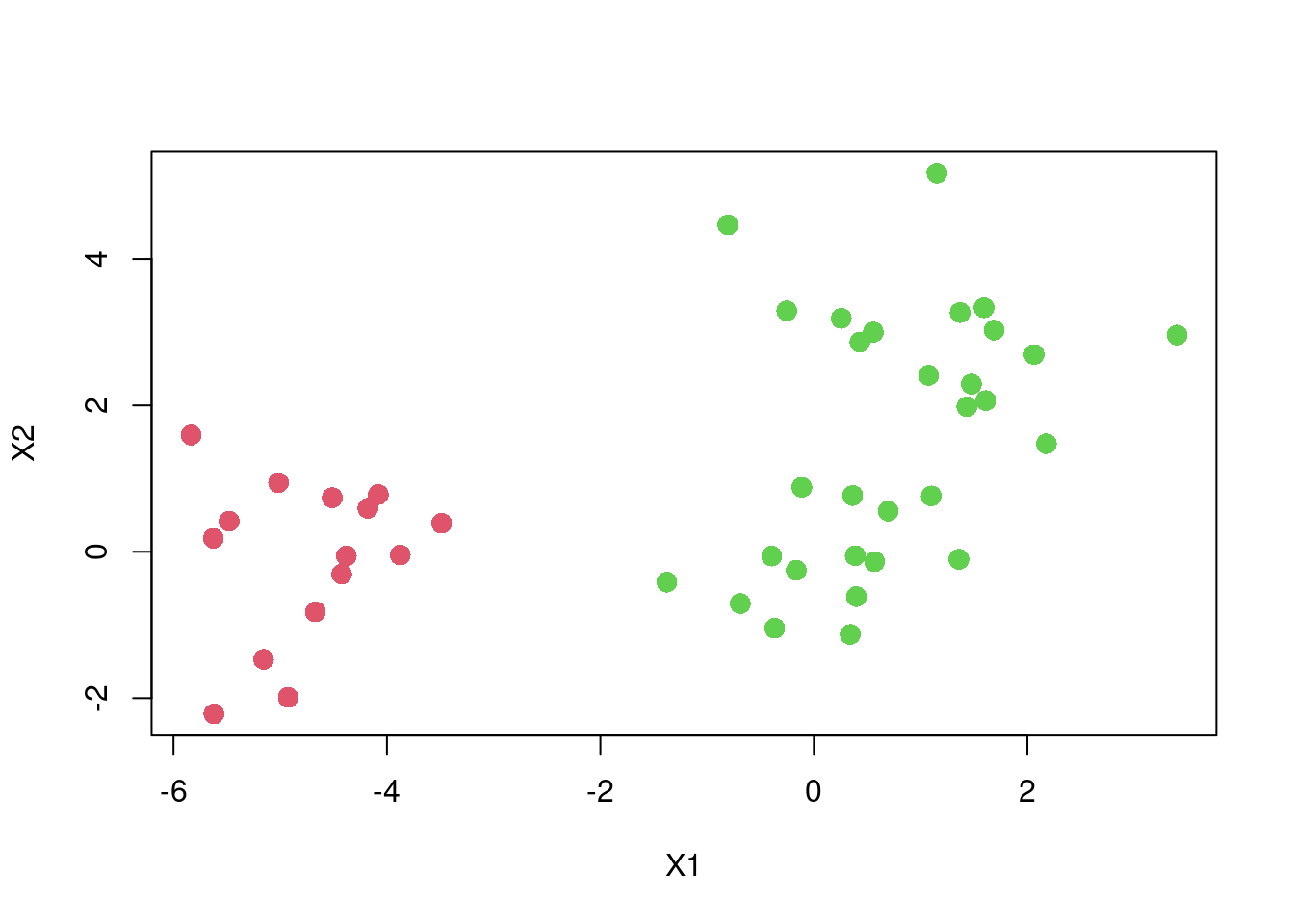
# plot with dots or labels
plot(X2 ~ X1, dat,
col = cutree(fit, k = 2) + 1,
pch = 16, cex=1.5)
#plot(X2 ~ X1, dat, type = "n")
#text(X2 ~ X1, dat,
# col = cutree(fit, k = 3) + 1,
# labels = rownames(dat))
# cut to get 3 clusters
fit |>
as.dendrogram() |>
# dendextend::set("branches_k_col", 2:4, k=3) |>
dendextend::set("labels_col", 2:4, k=3) |>
dendextend::set("labels_cex", 0.6) |>
plot()
abline(h = 5, lty = 2)
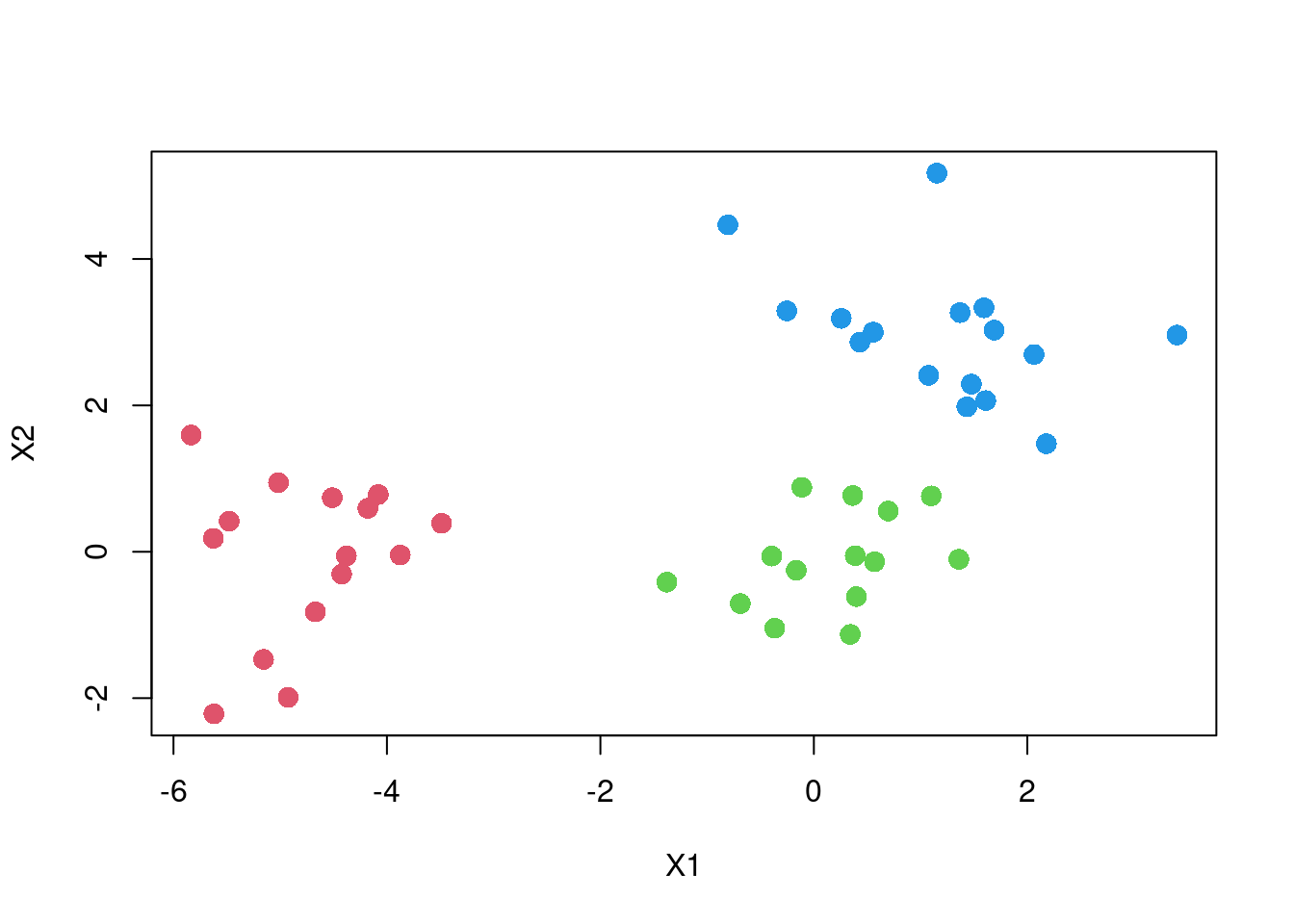
# plot with dots or labels
plot(X2 ~ X1, dat,
col = cutree(fit, k = 3) + 1,
pch = 16, cex=1.5)
#plot(X2 ~ X1, dat, type = "n")
#text(X2 ~ X1, dat,
# col = cutree(fit, k = 3) + 1,
# labels = rownames(dat))
# use package dendextend to color leaves and possibly branches
# https://talgalili.github.io/dendextend/articles/dendextend.html
# http://www.sthda.com/english/wiki/beautiful-dendrogram-visualizations-in-r-5-must-known-methods-unsupervised-machine-learning 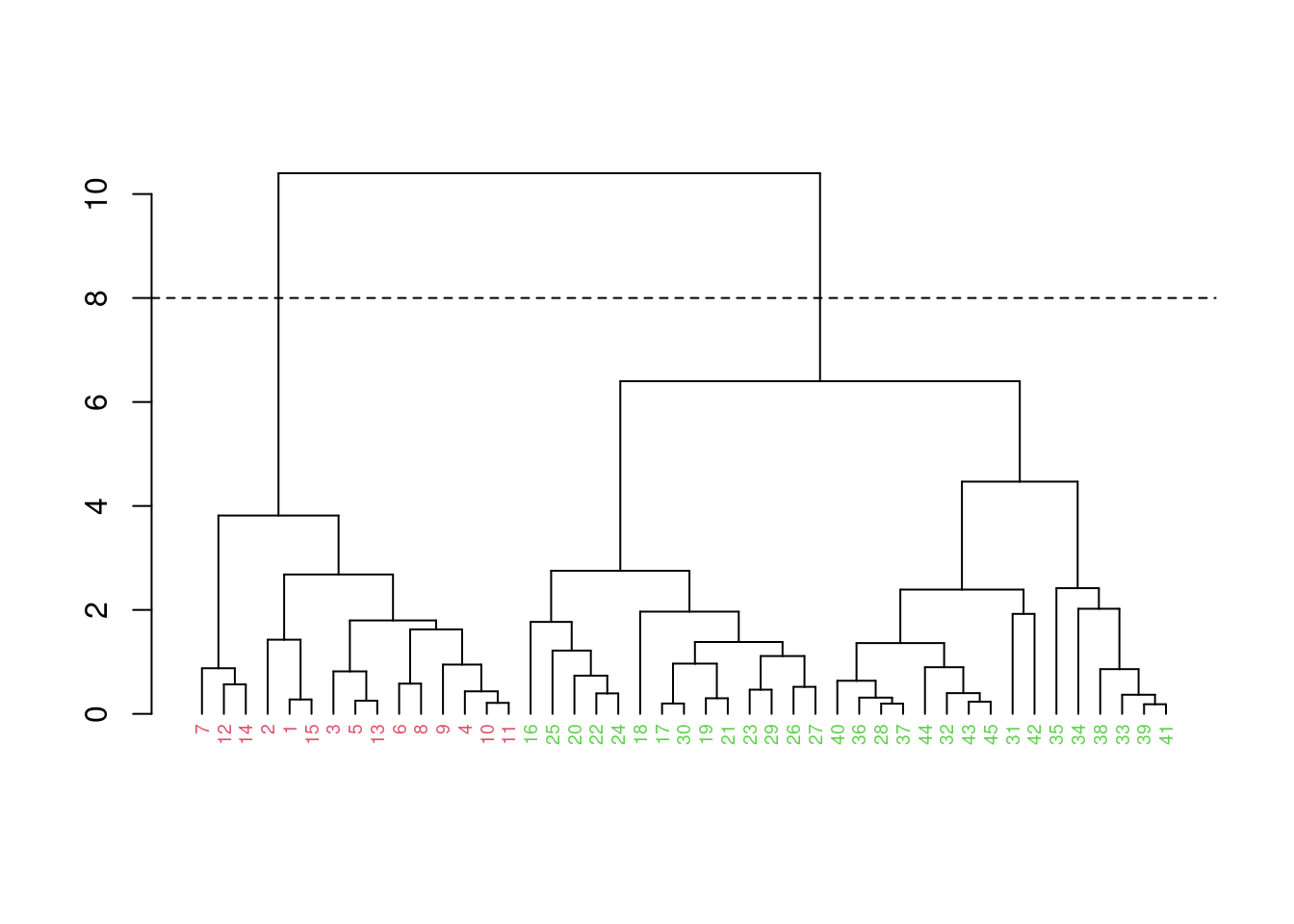
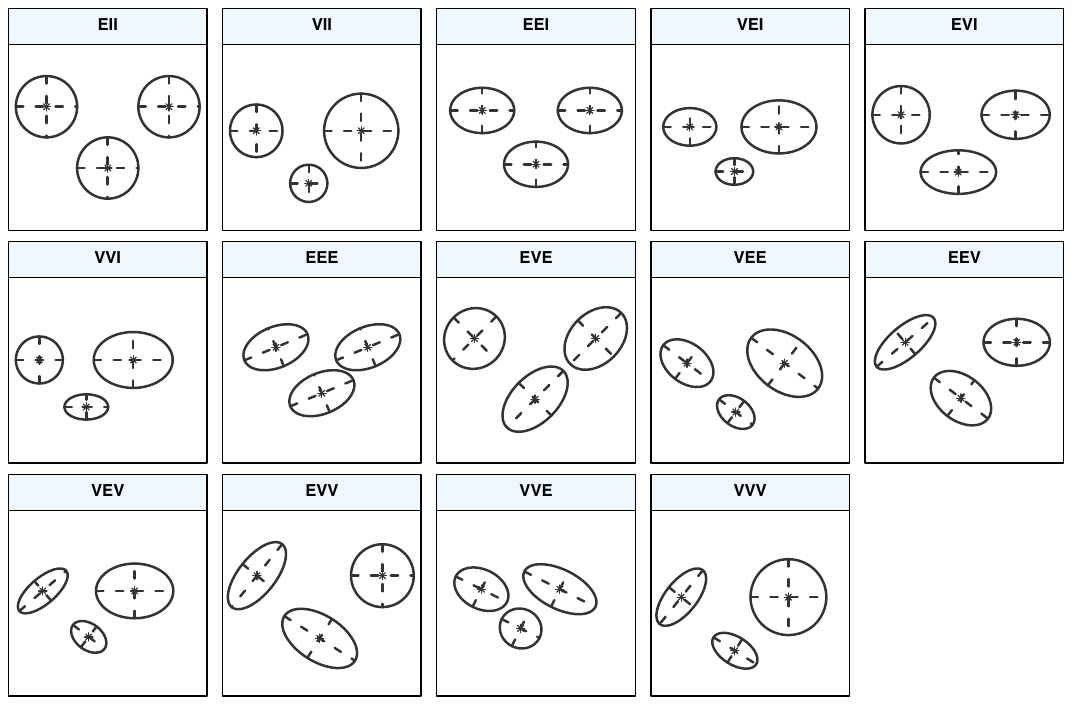
| Model | \mathbf{\Sigma}_k | Distribution | Volume | Shape | Orientation |
|---|---|---|---|---|---|
| EII | \lambda\mathbf{I} | Spherical | Equal | Equal | — |
| VII | \lambda_k\mathbf{I} | Spherical | Variable | Equal | — |
| EEI | \lambda\mathbf{A} | Diagonal | Equal | Equal | Coordinate axes |
| VEI | \lambda_k\mathbf{A} | Diagonal | Variable | Equal | Coordinate axes |
| EVI | \lambda\mathbf{A}_k | Diagonal | Equal | Variable | Coordinate axes |
| VVI | \lambda_k\mathbf{A}_k | Diagonal | Variable | Variable | Coordinate axes |
| EEE | \lambda\mathbf{D}\mathbf{A}\mathbf{D}^\intercal | Ellipsoidal | Equal | Equal | Equal |
| EVE | \lambda\mathbf{D}\mathbf{A}_k\mathbf{D}^\intercal | Ellipsoidal | Equal | Variable | Equal |
| VEE | \lambda_k\mathbf{D}\mathbf{A}\mathbf{D}^\intercal | Ellipsoidal | Variable | Equal | Equal |
| VVE | \lambda_k\mathbf{D}\mathbf{A}_k\mathbf{D}^\intercal | Ellipsoidal | Variable | Variable | Equal |
| EEV | \lambda\mathbf{D}_k\mathbf{A}\mathbf{D}_k^\intercal | Ellipsoidal | Equal | Equal | Variable |
| VEV | \lambda_k\mathbf{D}_k\mathbf{A}\mathbf{D}_k^\intercal | Ellipsoidal | Variable | Equal | Variable |
| VVV | \lambda_k\mathbf{D}_k\mathbf{A}_k\mathbf{D}_k^\intercal | Ellipsoidal | Variable | Variable | Variable |
Ďalšími ordinačnými metódami sú napr. principal coordinate analysis (PCoA) resp. multidimensional scaling (MDS), uniform manifold approximation and projection for dimension reduction (UMAP), t-distributed stochastic neighbor embedding (t-SNE)…↩︎