library(ggplot2)
data(sim1, package = "modelr")
sim1 |>
ggplot() + aes(x,y) + geom_point()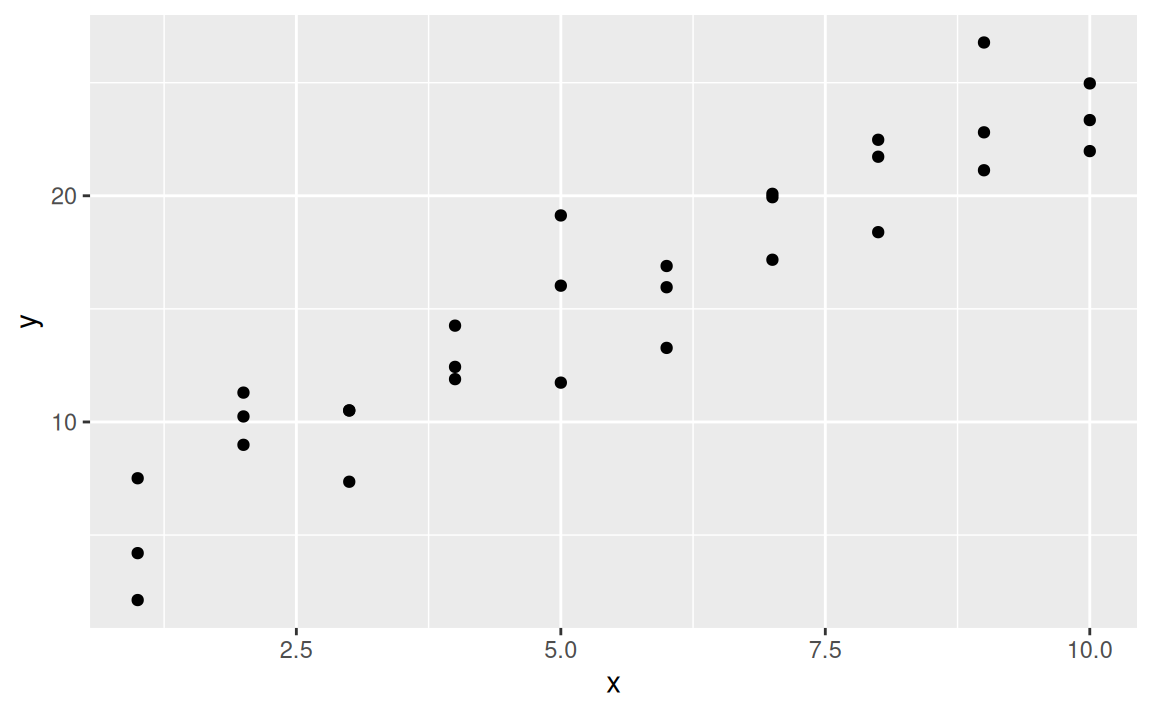
7 Modelovanie
Téma modelovania je inšpirovaná najmä knihou Wickham a Grolemund (2016), kapitolami 23 a 24.
7.1 Úvod
Cieľom modelovania je získať jednoduchý súhrn dát. V ideálnom prípade model vystihne skutočný signál (vzorec generovaný skúmaným javom, angl. pattern) a vynechá šum (náhodné odchýlky, ktoré nás nezaujímajú, angl. noise).
Sú dva druhy modelov
- prediktívne, ktoré majú za úlohu predpovedať rozdelenie skúmanej náhodnej premennej;
- objavné, ktoré pomáhajú odhaliť zaujímavé súvislosti v dátach.
Modely je výhodné použiť ako súčasť prieskumnej analýzy údajov na generovanie otázok a hypotéz o pozorovanom jave, ich tradičné zameranie však spočíva v podpore vyvodenia záverov (angl. inference) o dátach či potvrdení pravdivosti hypotéz. Oba účely sa dajú aplikovať v jednej analýze, no treba pri tom zachovať kritické myslenie, a preto jedno pozorovanie:
- možno použiť iba na jeden účel (prieskum alebo potvrdenie), nie oba,
- pri prieskume sa môže použiť ľubovoľne veľa krát, no iba raz pre generovanie záveru.
Je dôležité neprepadnúť prílišnému nadšeniu a nepomiešať konfirmačnú analýzu s prieskumnou, musia zostať nezávislé. Preto sa dáta zvyknú rozdeliť na dve alebo tri časti, napr.:
- 60% poslúži na prieskum a trénovanie modelov; (angl. training set)
- 20% sa vyhradí na preverenie a porovnanie modelov, ale nie v automatizovanom procese; (angl. validation set)
- 20% je testovacia vzorka použitá iba raz, na testovanie hypotézy.
Výstavba modelu je zložená z dvoch krokov:
- Identifikácia. Najprv určíme triedu modelov, ktorá vystihuje špecifický typ signálu. Napr. či signál má tvar priamky, \(y = \beta_1 + \beta_2 x\), alebo tvar nejakej nelineárnej funkcie, napr. \(y = \beta_1 x^{\beta_2}\), kde hodnoty premenných \(x,y\) sú pozorované a (neznáme) parametre \(\beta_1, \beta_2\) vyjadrujú konkrétnu podobu závislosti medzi premennými.
- Odhad. Následne nájdeme taký model zo zvolenej triedy, ktorý sa pozorovaným dátam najviac podobá, napr. \(y = 7 + 3x\) alebo \(y = 9 x^2\).
To znamená, že z danej triedy vyberieme najlepší model (podľa určitého kritéria). Neznamená to však, že tento model je dobrý, a už vôbec nie, že je správny (pravdivý).
„All models are wrong, but some are useful.” (G.Box)1
Zmysel modelu nie je odhaliť (celú) pravdu, skôr objaviť také zjednodušenie (aproximáciu), ktoré by bolo na konkrétny účel užitočné.
Modelovanie je veľmi komplexná téma. My sa budeme venovať tomu (v inžinierskej praxi) tradičnejšiemu – prediktívnemu modelovaniu – a aj to iba na prieskumné účely. Tiež nepôjdeme hlboko do matematických základov štatistického modelovania, postačí intuitívne chápanie ich fungovania a niekoľko užitočných nástrojov na to, aby sme pomocou modelov lepšie pochopili pozorované údaje.
7.2 Hľadanie najlepšieho modelu
Pomocou modelu teda dokážeme dáta rozložiť na signál (systematický vzorec správania) a šum. Čím viac vrstiev signál obsahuje, tým zložitejší model je potrebný na ich oddelenie. Na začiatok si vystačíme s jednoduchými, simulovanými údajmi.
Okrem pipe operátora a grafiky ggplot2 budeme používať funkcie a ilustračné súbory údajov balíka modelr, ktorý tiež zdiela princípy systému balíkov tidyverse. Prvý dataset obsahuje dve spojité premenné, x a y:
V dátach zreteľne vidno signál, ten sa pokúsime vystihnúť modelom. Vzťah medzi premennými vyzerá lineárne, preto všeobecný tvar modelu by mohol byť \(y = b_1 + b_2x\). Vygenerujme náhodne sto modelov z tejto triedy:
set.seed(1)
models <- data.frame(
b1 = runif(100, -20, 40),
b2 = runif(100, -5, 5)
)
ggplot(sim1) + aes(x, y) +
geom_abline(aes(intercept = b1, slope = b2), data = models, alpha = 1/4) +
geom_point()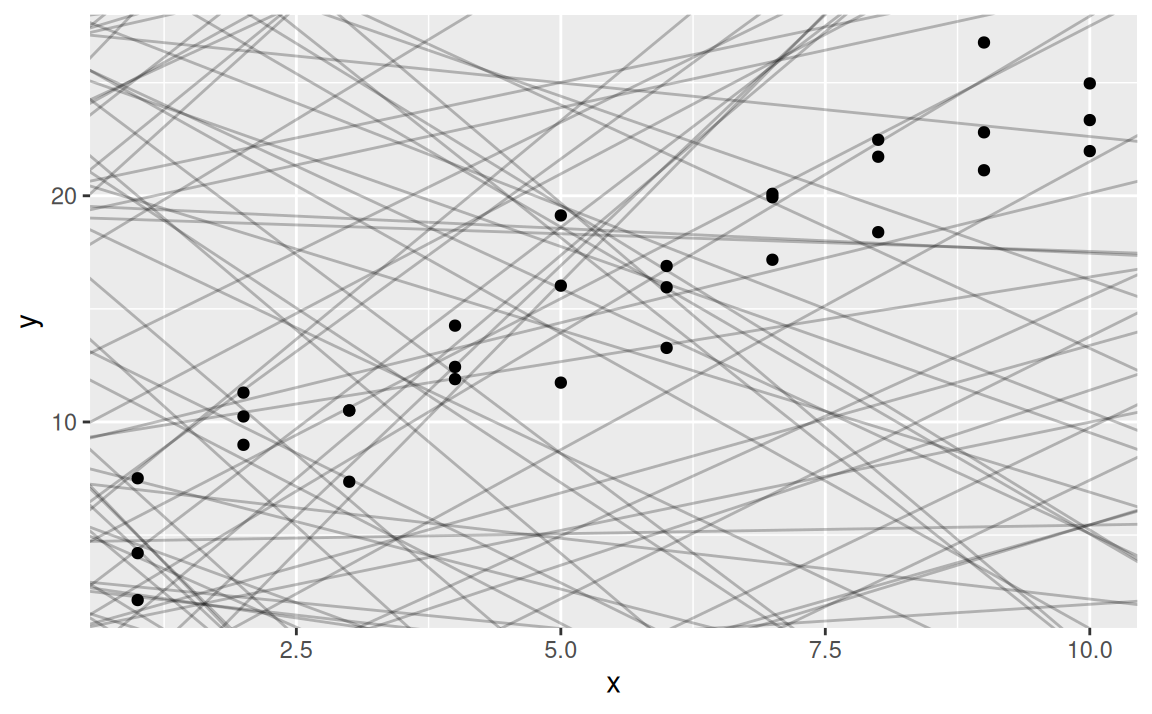
Väčšina z modelov je vyslovene zlá. Aby sme našli dobrý model, musíme zadefinovať, čo to znamená, že model „vystihuje” dáta, že je k nim „blízko”. Až potom nájdeme jeho parametre \(b_1,b_2\).
Jedným z možných kritérií je vertikálna vzdialenosť medzi pozorovaniami a modelovými hodnotami (predikciami, bodmi na priamke):
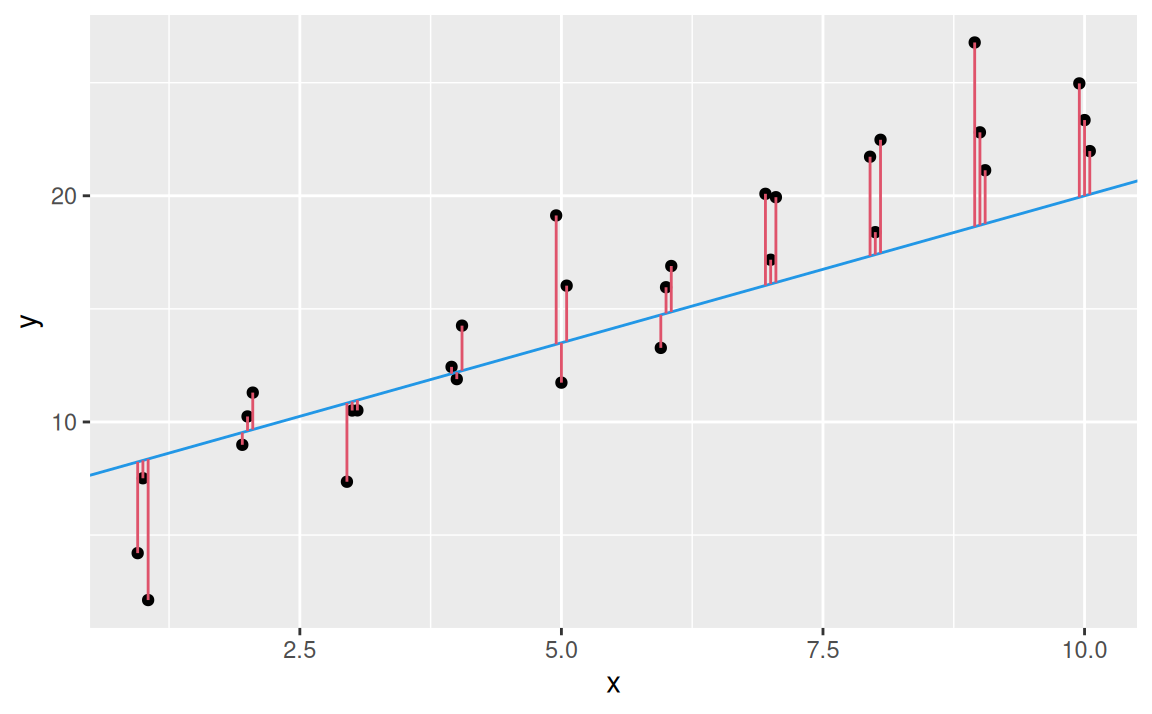
Na výpočet vzdialenosti v R je jednoduchšie mať triedu modelov vo forme funkcie. Pomocou nej dostaneme predikcie v každom bode premennej \(x\).
model1 <- function(b, data) b[1] + b[2] * data$x
model1(c(7,1.3), sim1) # predikcie z horného obrázku [1] 8.3 8.3 8.3 9.6 9.6 9.6 10.9 10.9 10.9 12.2 12.2 12.2 13.5 13.5 13.5
[16] 14.8 14.8 14.8 16.1 16.1 16.1 17.4 17.4 17.4 18.7 18.7 18.7 20.0 20.0 20.0Z nich sa vypočíta 30 hodnôt vertikálnej vzdialenosti medzi pozorovaniami a predikciami. Na ohodnotenie modelu však treba iba jedno číslo, čiže potrebujeme nejakú mieru celkovej vzdialenosti. V štatistike sa (kvôli viacerým dobrým matematickým vlastnostiam) najčastejšie používa odmocnina zo strednej kvadratickej odchýlky (angl. root mean squared error, RMSE):
measure_distance <- function(b, data) {
diff <- data$y - model1(b, data)
sqrt(mean(diff ^ 2))
}
measure_distance(c(7, 1.3), sim1)[1] 3.320056Pomocou funkcie map2 z balíku purrr2, ktorá je dvojrozmernou a bezpečnejšou alternatívou ku funkcii mapply, vypočítame vzdialenosť pre všetky naše náhodné modely a zobrazíme desať najlepších modelov (t.j tých s najmenšou vzdialenosťou):
models <- models |>
transform(dist = purrr::map2_dbl(
b1, b2,
.f = function(x,y) measure_distance(c(x,y), sim1)
)) |>
dplyr::arrange(dist)
models |> head() |> round(2) b1 b2 dist
1 3.40 2.41 2.63
2 -0.06 2.80 3.03
3 8.66 1.15 3.40
4 8.92 0.75 4.96
5 -3.97 2.55 6.03
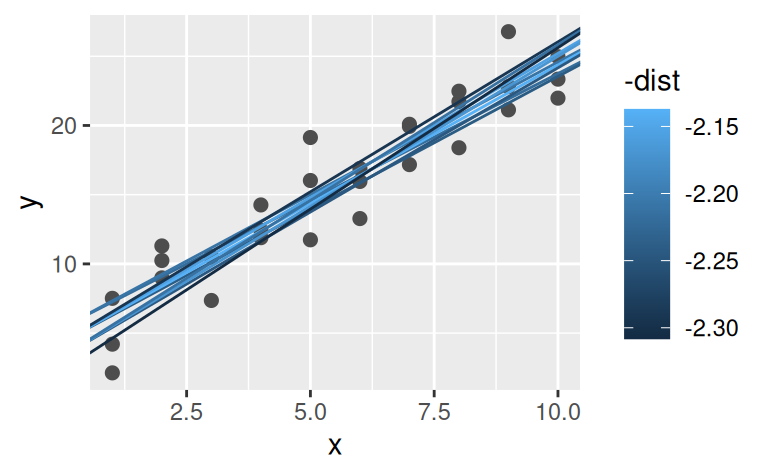
6 0.80 3.56 6.87ggplot(sim1, aes(x, y)) +
geom_point(size = 2, colour = "grey30") +
geom_abline(
aes(intercept = b1, slope = b2, colour = -dist),
data = dplyr::filter(models, rank(dist) <= 10)
)
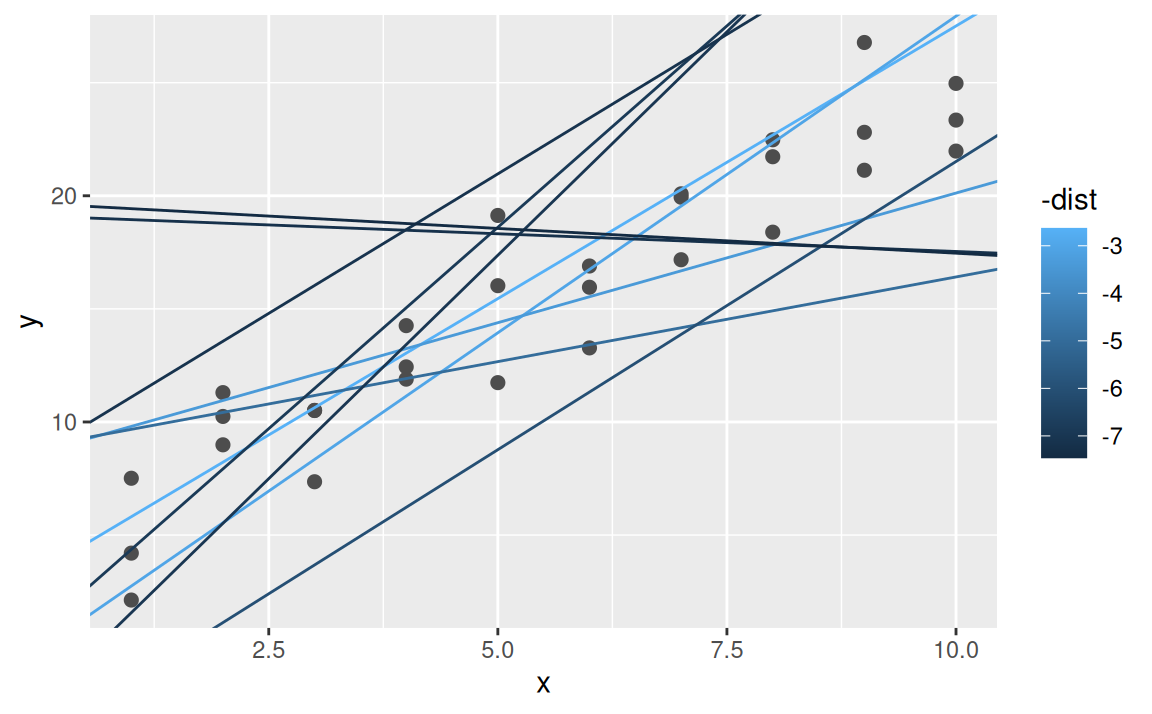
Modely sa dajú znázorniť aj ako body v priestore parametrov. Skupina desiatich najlepších modelov je zvýraznená červenou farbou.
models |>
ggplot() + aes(b1, b2) +
geom_point(data = dplyr::filter(models, rank(dist) <= 10), size = 4, colour = 2) +
geom_point(aes(colour = -dist))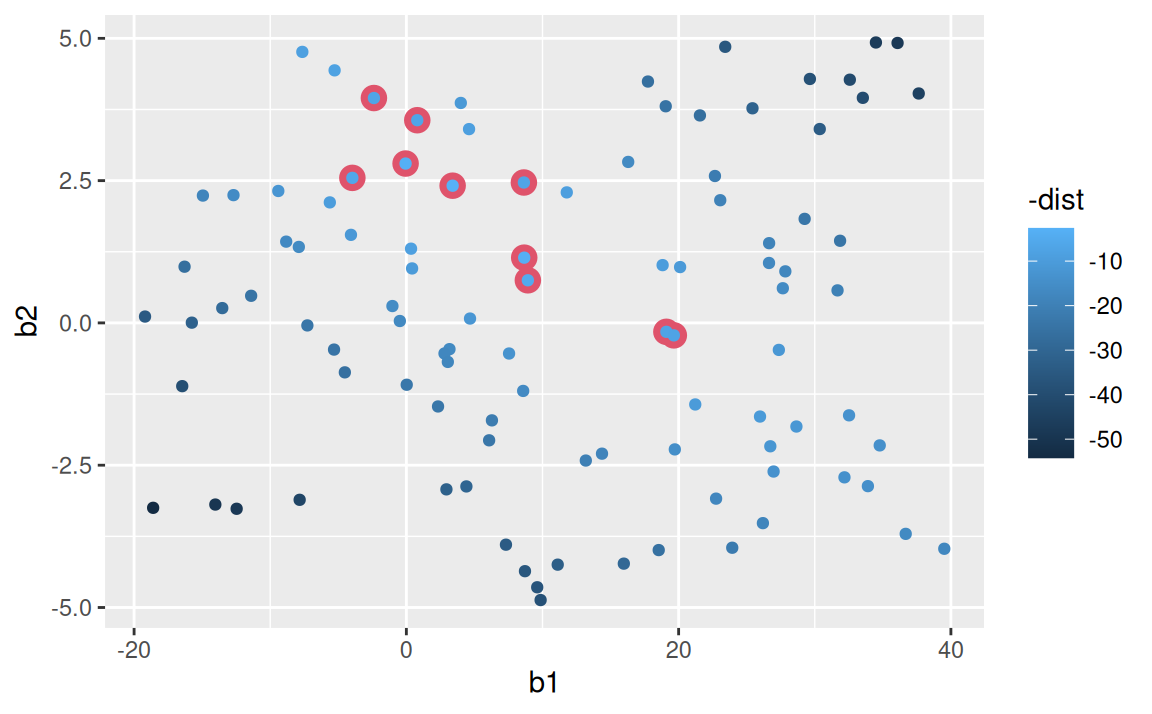
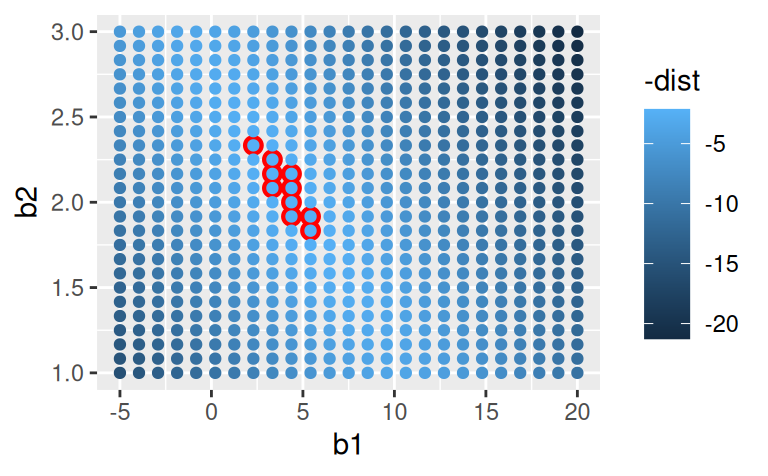
Namiesto skúšania množstva náhodných modelov je systematickejším prístupom hľadanie parametrov „ideálneho” modelu v pravidelnej mriežke. Potom desať najlepších modelov bude v pôvodnom priestore (\(x,y\)) vyzerať podstatne lepšie:
grid <- expand.grid(
b1 = seq(-5, 20, length = 25),
b2 = seq(1, 3, length = 25)
) |>
transform(
dist = purrr::map2_dbl(b1, b2, function(x,y) measure_distance(c(x,y), sim1))
)
ggplot(data = grid) + aes(b1, b2) +
geom_point(data = dplyr::filter(grid, rank(dist) <= 10), size = 3, colour = "red") +
geom_point(aes(colour = -dist))
ggplot(data = sim1) + aes(x, y) +
geom_point(size = 2, colour = "grey30") +
geom_abline(
aes(intercept = b1, slope = b2, colour = -dist),
data = dplyr::filter(grid, rank(dist) <= 10)
)
Mriežku by sme mohli ďalej zjemňovať, až by sme narazili na najlepší model. Je však aj pohodlnejšia cesta: Newton-Raphsonova metóda numerickej optimalizácie. Hľadanie globálneho minima (funkcie vzdialenosti) v nej funguje tak, že v priestore parametrov sa zvolí počiatočný bod, nájde sa smer najväčšieho klesania (gradient funkcie), v jeho smere sa o kúsok nižšie zvolí ďalší bod a celý proces sa zopakuje. Keď už sa nedá ísť nižšie, našli sme minimum, ktorého súradnice predstavujú hodnoty parametrov najlepšieho modelu. V Rku s riešením optimalizačnej úlohy pomôže funkcia optim:
best <- optim(par = c(0, 0),
fn = measure_distance,
data = sim1)
best$par[1] 4.222248 2.051204ggplot(sim1, aes(x, y)) +
geom_point(size = 2, colour = "grey30") +
geom_abline(intercept = best$par[1], slope = best$par[2], color = 4)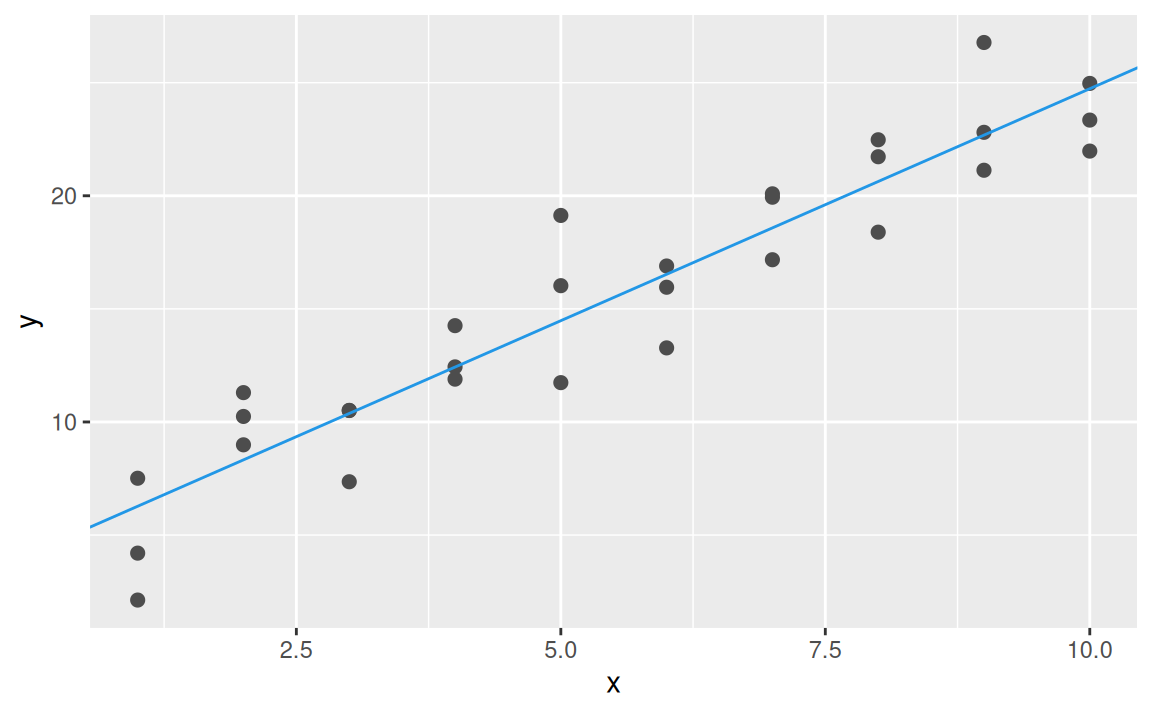
Takto sa dajú odhadnúť parametre modelu z akejkoľvek triedy modelov, stačí poznať rovnicu triedy a pomocou nej definovať účelovú funkciu. V tomto prípade to bola miera vzdialenosti (ktorú minimalizujeme), v inej metóde je to tzv. vierohodnosť (ktorú, naopak, je potrebné maximalizovať).
Všeobecný zápis triedy lineárnych modelov (pre ľubovoľný počet premenných \(x_i\)) je \[ y = b_1 + b_2x_1 + \ldots + b_px_{p-1} \] a dá sa prepísať do tvaru skalárneho súčinu (vektoru parametrov a vektoru bázových funkcií) \[ y = (b_1, b_2,\ldots,b_p)\cdot (1,x_1,\ldots,x_{p-1}). \] Vďaka tomu je možné parametre lineárnych modelov odhadnúť aj jednoduchším a rýchlejším spôsobom – pomocou nástrojov lineárnej algebry. V Rku na to slúži funkcia stats::lm, kde pomocou tzv. formuly (s ktorou sme sa už stretli pri zobrazovaní) stačí špecifikovať vzťah medzi premennými:
mod1 <- lm(formula = y ~ x, data = sim1)
coef(mod1)(Intercept) x
4.220822 2.051533 Označením Intercept sa vždy myslí tzv. absolútny člen v rovnici modelu, teda člen, ktorý neobsahuje žiadnu premennú (iba konštantu 1).
Parametre lineárneho modelu sa okrem jednoduchého odhadu aj jednoducho interpretujú: ak hodnota premennej \(x\) nadobudne nulovú hodnotu, stredná hodnota premennej \(y\) bude 4.22, a ak sa \(x\) zmení o 1, premenná \(y\) sa „v priemere” zmení o 2.05.
7.3 Predpovede a rezíduá
Štúdiom stochastického modelu a jeho parametrov sa dopodrobna zaoberá matematická štatistika. Nám bude zatiaľ stačiť zbežný pohľad na jeho predpoveď (predikciu, čiže strednú hodnotu odozvy \(y\) podmienenú hodnotami prediktorov \(x_1,\ldots,x_{p-1}\)) a zvyšok po modelovaní (rezíduum).
Pri vizualizáci predikcií je vhodné začať vytvorením rovnomernej mriežky bodov premennej \(x\). V Rku najľahšie asi pomocou funkcie modelr::data_grid. Následne pridáme predikcie vypočítané z nášho modelu
grid <- sim1 |>
modelr::data_grid(x) |>
modelr::add_predictions(mod1) |> # alebo: transform(pred = predict(mod1))
print()# A tibble: 10 × 2
x pred
<int> <dbl>
1 1 6.27
2 2 8.32
3 3 10.4
4 4 12.4
5 5 14.5
6 6 16.5
7 7 18.6
8 8 20.6
9 9 22.7
10 10 24.7 a vykreslíme ich.
ggplot(sim1, aes(x)) +
geom_point(aes(y = y)) +
geom_line(aes(y = pred), data = grid, colour = 4, linewidth = 1)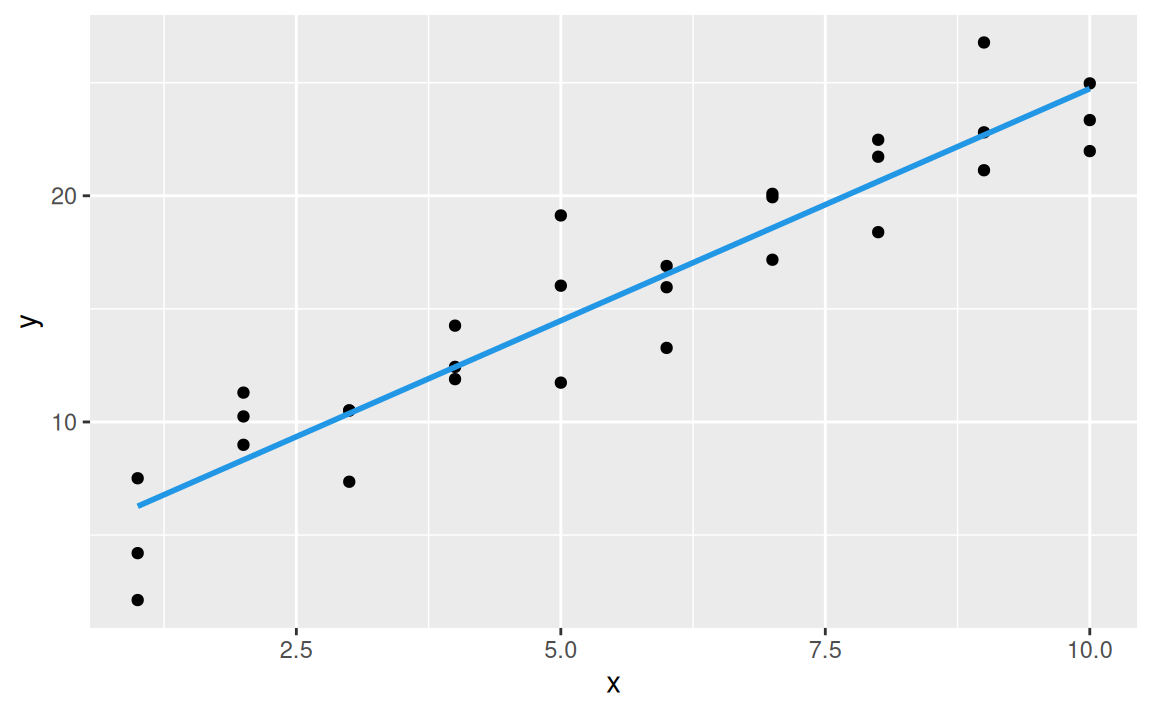
Funkcia modelr::add_predictions na pozadí používa pre výpočet predikcií základnú funkciu stats::predict. Pomocou nej teraz vypočítame strednú hodnotu premennej \(y\) podľa modelu mod1, ak \(x = 2.5\):
predict(mod1, newdata = data.frame(x = 2.5)) 1
9.349655 Opačnú stranu mince predstavujú rezíduá, teda to, čo model v dátach nedokázal vystihnúť. Matematicky vyjadrujú rozdiel medzi pozorovanými a predpovedanými hodnotami. Okrem diagnostiky modelu nám umožňujú upriamiť pozornosť na menej výraznú zložku signálu v dátach.
sim1 <- sim1 |>
modelr::add_residuals(mod1) |> # alebo: transform(resid = residuals(mod1))
print()# A tibble: 30 × 3
x y resid
<int> <dbl> <dbl>
1 1 4.20 -2.07
2 1 7.51 1.24
3 1 2.13 -4.15
4 2 8.99 0.665
5 2 10.2 1.92
6 2 11.3 2.97
7 3 7.36 -3.02
8 3 10.5 0.130
9 3 10.5 0.136
10 4 12.4 0.00763
# ℹ 20 more rowsggplot(sim1) + aes(resid) +
geom_histogram(binwidth = 0.5)
ggplot(sim1) + aes(x, resid) +
modelr::geom_ref_line(h = 0) +
geom_point()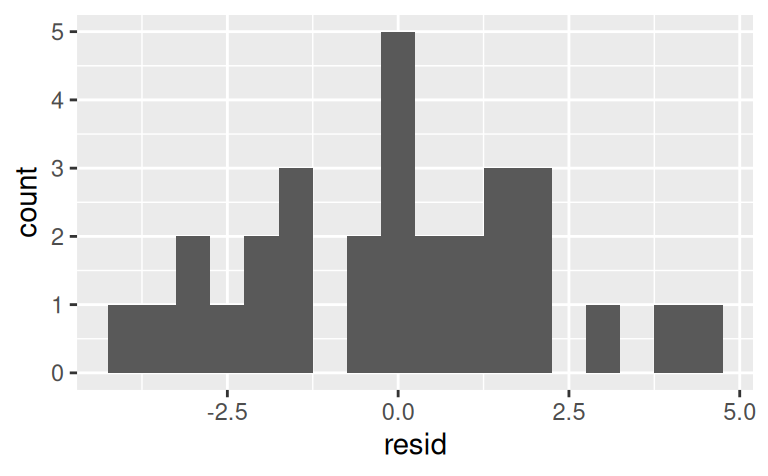 
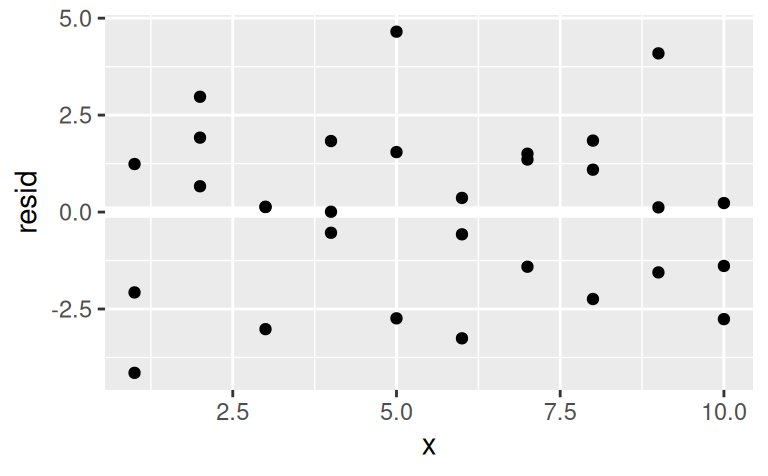
Naše rezíduá vyzerajú byť normálne rozdelené (čo je výhodné pri konštrukcii predpovedných intervalov) a aj náhodne rozptýlené okolo nuly, takže model si svoju úlohu (zachytiť signál) splnil dobre.
7.4 Špecifiká lineárneho modelu
7.4.1 Formula
Väčšina modelovacích funkcií v R používa formuly. V našom jednoduchom príklade sme videli, že softvér previedol formulu
y ~ x
na rovnicu \[ \begin{split} y &= b_1+b_2x \\ &= (b_1,b_2)\cdot(1,x) \end{split} \] pričom absolútny člen do nej pridal automaticky.
Vektor bázových funkcií \((1,x)\) tvorí riadky tzv. matice plánu \(\mathbf{X}\) (angl. design matrix), s ktorou sa pomocou vzťahu \[ (b_1, b_2)^T=(\mathbf{X}^T\mathbf{X})^{-1}\mathbf{X}^T\mathbf{y} \] získa odhad parametrov najlepšieho modelu. Vektor \(\mathbf{y}\) obsahuje pozorované hodnoty premennej \(y\), čiže \(\mathbf{y}=( 4.2,7.51,2.13,8.99 ,...)^T\). Maticu plánu \(\mathbf{X}\) nám z formuly zostaví funkcia stats::model.matrix alebo vo formáte tibble funkcia modelr::model_matrix:
sim1 |>
modelr::model_matrix(y ~ x)# A tibble: 30 × 2
`(Intercept)` x
<dbl> <dbl>
1 1 1
2 1 1
3 1 1
4 1 2
5 1 2
6 1 2
7 1 3
8 1 3
9 1 3
10 1 4
# ℹ 20 more rows7.4.2 Kvalitatívne premenné
Generovanie vzťahu z formuly je priamočiare, ak sú vysvetľujúce premenné kvantitatívne (numerické). Situácia sa však skomplikuje s pridaním kvalitatívneho prediktoru. Takým je premenná \(x\) v ilustračnom datasete sim2, pretože nadobúda iba 4 nečíselné hodnoty \(a,b,c,d\):
data(sim2, package = "modelr")
sim2# A tibble: 40 × 2
x y
<chr> <dbl>
1 a 1.94
2 a 1.18
3 a 1.24
4 a 2.62
5 a 1.11
6 a 0.866
7 a -0.910
8 a 0.721
9 a 0.687
10 a 2.07
# ℹ 30 more rowsggplot(sim2) + aes(x, y) + geom_point()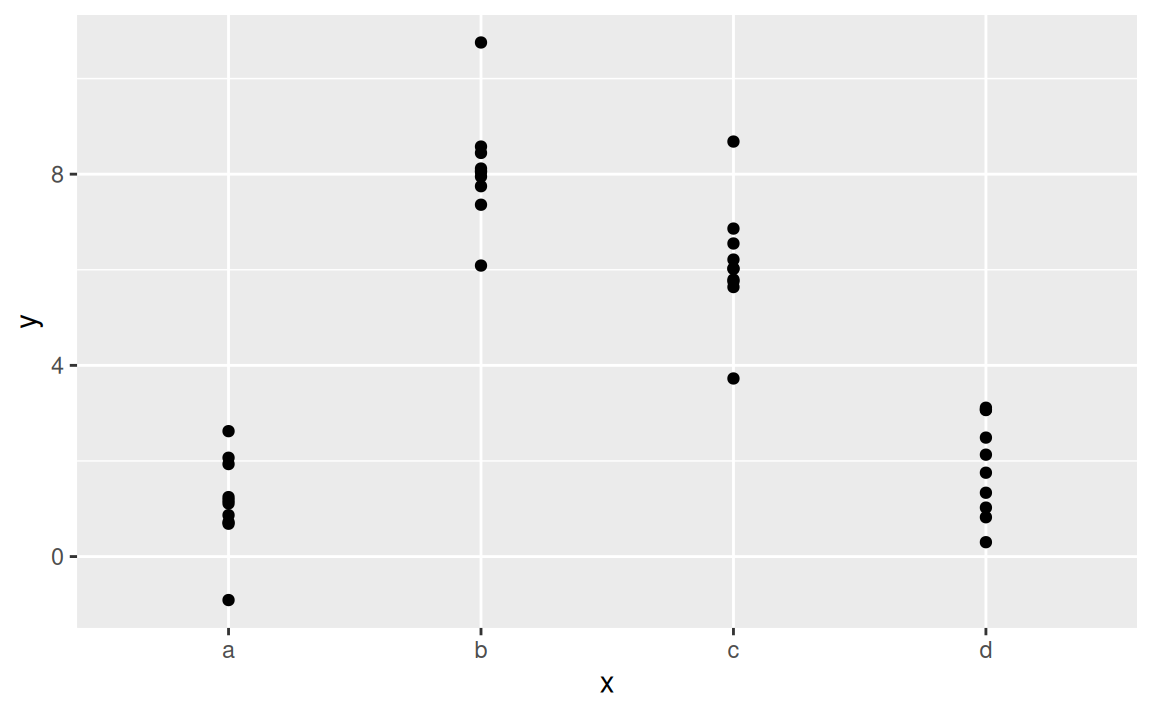
Opäť sa dá použiť lineárny model na určenie strednej hodnoty vysvetľovanej premennej \(y\) v závislosti od vysvetľujúcej premennej \(x\):
mod2 <- lm(y ~ x, data = sim2)
mod2
Call:
lm(formula = y ~ x, data = sim2)
Coefficients:
(Intercept) xb xc xd
1.1522 6.9639 4.9750 0.7588 grid <- sim2 |>
modelr::data_grid(x) |>
modelr::add_predictions(mod2)
grid# A tibble: 4 × 2
x pred
<chr> <dbl>
1 a 1.15
2 b 8.12
3 c 6.13
4 d 1.91ggplot(sim2) + aes(x) +
geom_point(aes(y = y)) +
geom_point(data = grid, aes(y = pred), colour = 4, size = 4)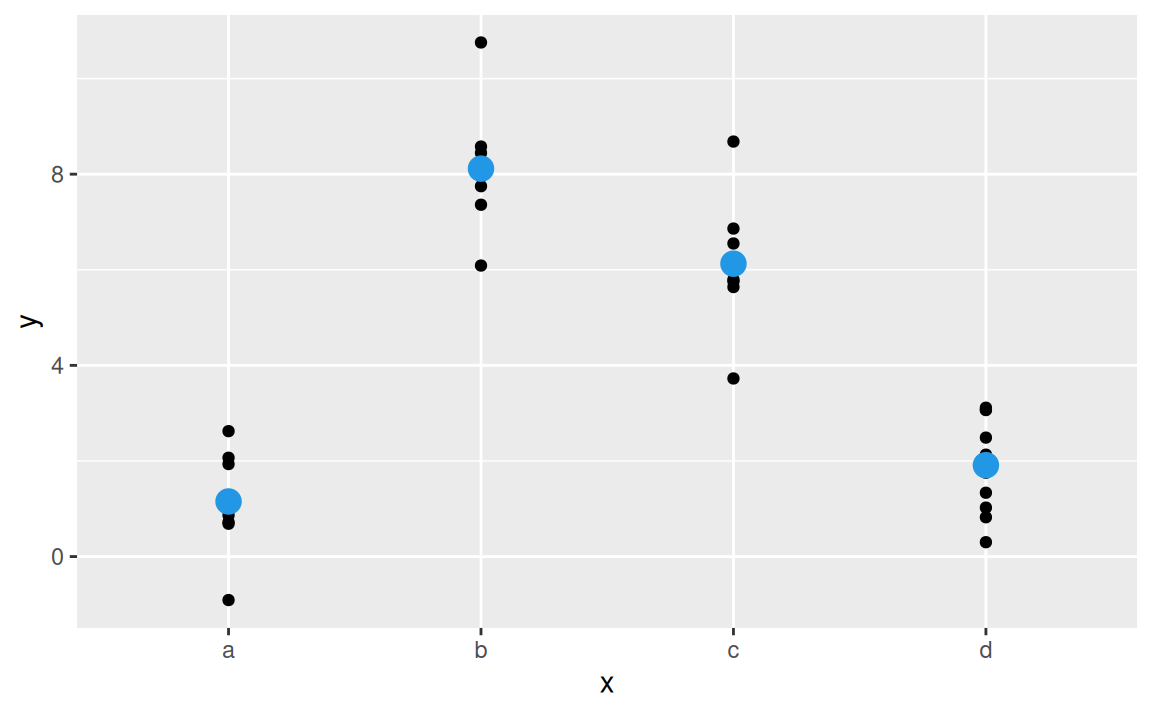
ktorý vypočíta aritmetický priemer \(y\) v každej kategórii \(x\) (pretože priemer minimalizuje štvorec vzdialenosti). Zápis rovnice modelu je oproti formule komplikovanejší, \[ y = b_1 + b_2 x_b + b_3 x_c + b_4 x_d, \] pretože namiesto \(x\) obsahuje tri pomocné, binárne premenné, ktoré nadobúdajú hodnoty 0 alebo 1. Napr. \[ x_b = \begin{cases} 1 & \text{ak}\quad x=b, \\ 0 & \text{inak} \end{cases} \] Hodnota parametra \(b_1=1.15\) sa rovná strednej hodnote \(y\) v kategórii \(x=a\), všetky ostatné parametre predstavujú prírastok oproti prvej kategórii, napr. priemer v kategórii \(x=c\) sa rovná \(b_1+b_3=6.13\).
Treba si ešte uvedomiť, že modelom s kvalitatívnou premennou nie je možné urobiť predikcie pre kategóriu, na ktorej model nebol natrénovaný:
predict(mod2, newdata = data.frame(x = "e"))Error in model.frame.default(Terms, newdata, na.action = na.action, xlev = object$xlevels): factor x has new level e7.4.3 Interakcie
Majme teraz dve vysvetľujúce premenné. Jedna je spojitá (\(x_1\)), druhá kategorická (\(x_2\)).
data(sim3, package = "modelr")
ggplot(sim3) + aes(x1, y) + geom_point(aes(colour = x2))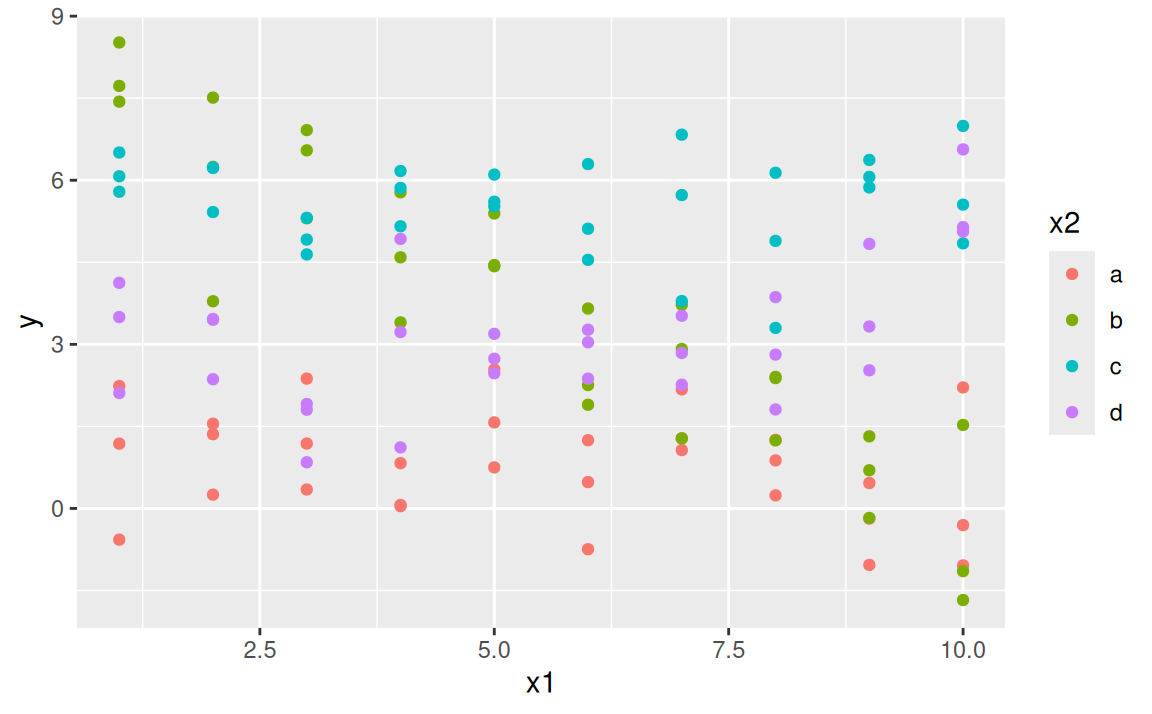
Tu máme na výber z dvoch lineárnych modelov:
mod1 <- lm(y ~ x1 + x2, data = sim3)
mod2 <- lm(y ~ x1 * x2, data = sim3)Keď prediktory spojíme operátorom +, model popíše vplyv každej premennej na odozvu nezávisle od tej druhej, vzťahom \(y = b_1 + b_2x_1 + b_3x_2\). Na druhej strane formula
y ~ x1 * x2
sa preloží do rovnice \[ y = b_1 + b_2x_1 + b_3x_2 + b_4x_1x_2. \] (Obe rovnice platia v prípade kategorickej premennej len schématicky, keďže \(x_2\) treba ešte rozložiť na pomocné binárne premenné \(x_{2b},x_{2c},x_{2d}\).) Posledný člen \(x_1x_2\) predstavuje tzv. interakciu. I keď model už nie je lineárny v premenných, stále je lineárny v parametroch, takže sa dá jednoducho odhadnúť.
Vizualizácia oboch modelov si vyžaduje prípravu predikcií v dvoch krokoch:
- konštrukcia dvojrozmernej mriežky (kombinácia hodnôt dvoch prediktorov),
- generovanie predikcií z oboch modelov v jednom dátovom rámci (gather_predictions ho vytvorí v dlhom formáte, spread_predictions v širokom).
grid <- sim3 |>
modelr::data_grid(x1, x2) |>
modelr::gather_predictions(mod1, mod2)
grid# A tibble: 80 × 4
model x1 x2 pred
<chr> <int> <fct> <dbl>
1 mod1 1 a 1.67
2 mod1 1 b 4.56
3 mod1 1 c 6.48
4 mod1 1 d 4.03
5 mod1 2 a 1.48
6 mod1 2 b 4.37
7 mod1 2 c 6.28
8 mod1 2 d 3.84
9 mod1 3 a 1.28
10 mod1 3 b 4.17
# ℹ 70 more rowsggplot(sim3, aes(x1, colour = x2)) +
geom_point(aes(y = y)) +
geom_line(data = grid, aes(y = pred)) +
facet_wrap(~ model)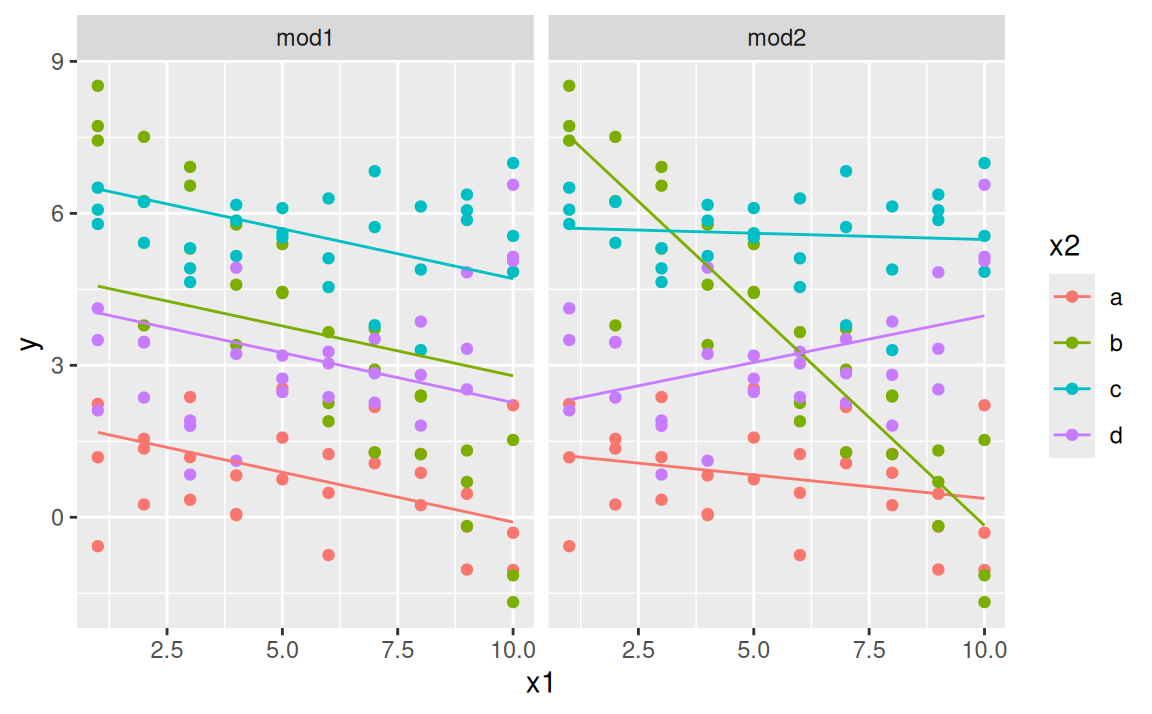
Oba modely majú v každej kategórii odlišný absolútny člen. Jednoduchší z modelov však má sklon priamok rovnaký, naproti tomu model s interakciou má odlišný aj sklon.
Ktorý model popisuje signál v týchto dátach lepšie? Pozrime na rezíduá odseparované vo fazetách podľa skupín:
sim3 <- sim3 |>
modelr::gather_residuals(mod1, mod2)
ggplot(sim3) + aes(x1, resid, colour = x2) +
geom_point() +
facet_grid(model ~ x2)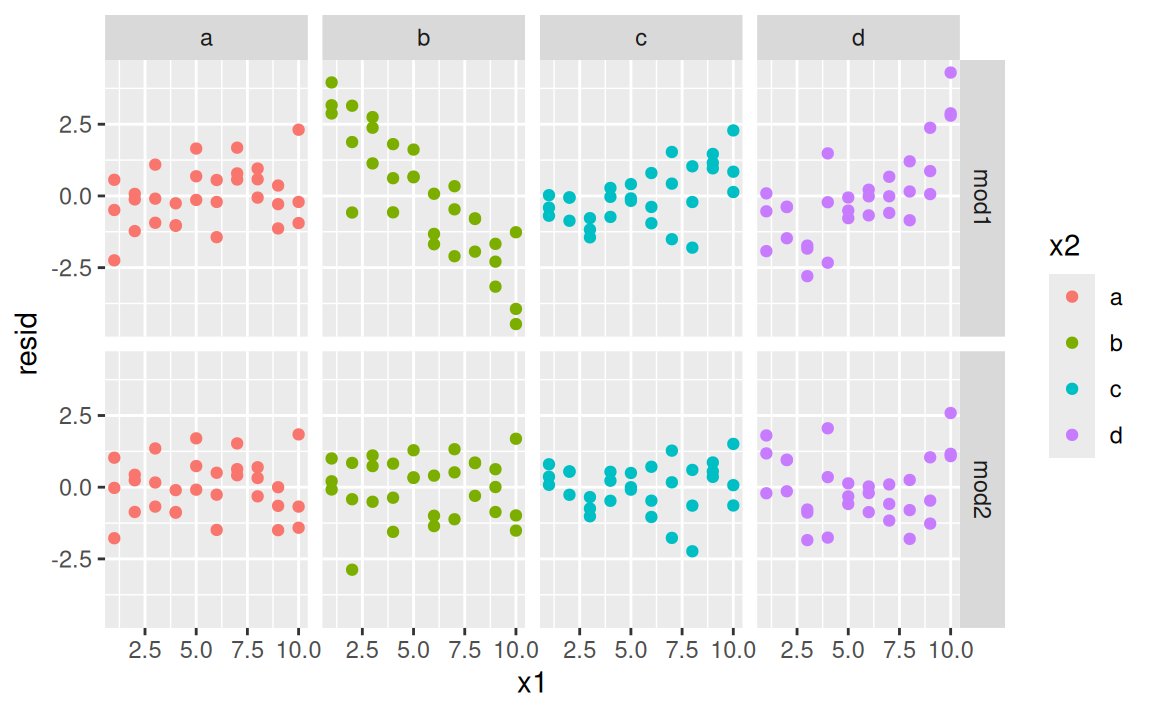
Rezíduá druhého modelu sa zdajú byť (takmer) náhodne rozptýlené okolo nuly, bez nejakého výrazného signálu. Zato prvému modelu unikol výrazný vzor (pattern) v skupine \(x_2=b\) a v menšej miere aj v ostatných skupinách. Čiže z pohľadu diagnostiky rezíduí je model mod2 lepší. Samozrejme, sú aj exaktnejšie metódy vyhodnotenia a porovnania modelov, tie však už svojim matematickým pozadím presahujú záber tohto kurzu. (V krátkosti sa im povenujeme neskôr.)
Prirodzene, interakcia môže existovať aj medzi spojitými premennými, rovnica modelu je vtedy jednoduchšia a pri vizualizácii musíme zvoliť úrovne jednotlivých rezov trojrozmernej funkcie. Použijeme ilustračný dataset sim4.
data(sim4, package = "modelr")
ggplot(sim4) + aes(x1, x2, color = y) + geom_jitter(width = 0.02, height = 0.02) +
scale_color_gradient2(low = "blue", mid = "green", high = "red")
ggplot(sim4) + aes(x2, y, color = x1) + geom_jitter(width = 0.02) +
viridis::scale_color_viridis(option = "D")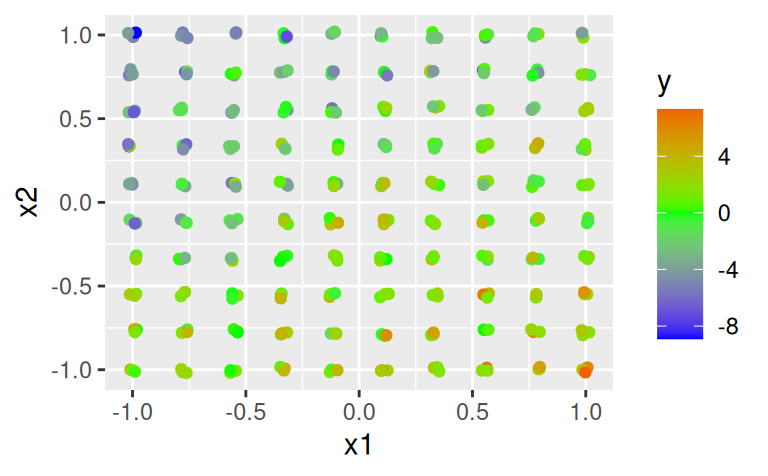
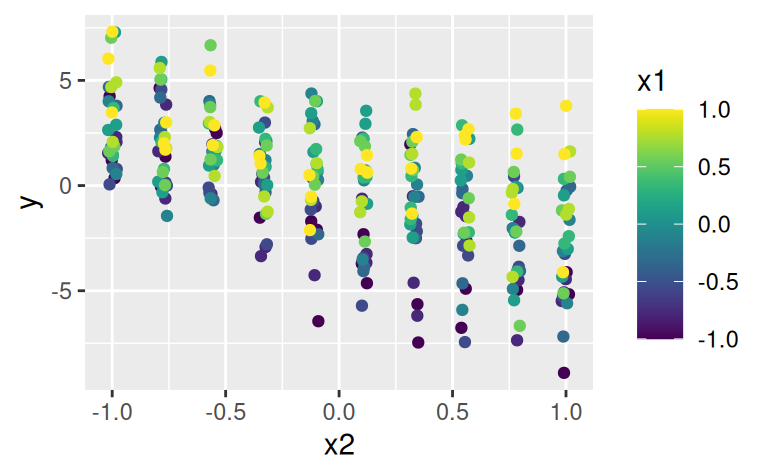
Zobrazenie trojrozmerných dát na spojitej mierke je pomerne málo názorné, tu sa dá pomôcť interaktívnym 3D grafom (nezobrazené):
plotly::plot_ly(sim4,
x=~x1, y=~x2, z=~y, color=~y, size = 2,
type = 'scatter3d', mode='markers',
colors = rev(RColorBrewer::brewer.pal(n = 8, name = "Spectral"))
)Modelovanie je podobné ako predtým, avšak diskretizáciu spojitého priestoru si teraz prispôsobíme pomocou funkcie seq_range.
mod1 <- lm(y ~ x1 + x2, data = sim4)
mod2 <- lm(y ~ x1 * x2, data = sim4)
grid <- sim4 |>
modelr::data_grid(
x1 = modelr::seq_range(x1, n = 5),
x2 = modelr::seq_range(x2, n = 5)
) |>
modelr::gather_predictions(mod1, mod2)
grid# A tibble: 50 × 4
model x1 x2 pred
<chr> <dbl> <dbl> <dbl>
1 mod1 -1 -1 0.996
2 mod1 -1 -0.5 -0.395
3 mod1 -1 0 -1.79
4 mod1 -1 0.5 -3.18
5 mod1 -1 1 -4.57
6 mod1 -0.5 -1 1.91
7 mod1 -0.5 -0.5 0.516
8 mod1 -0.5 0 -0.875
9 mod1 -0.5 0.5 -2.27
10 mod1 -0.5 1 -3.66
# ℹ 40 more rowsPredikcie sa dajú zobraziť podobne ako dáta, čiže zhora,
ggplot(grid, aes(x1, x2)) +
geom_tile(aes(fill = pred)) +
facet_wrap(~ model)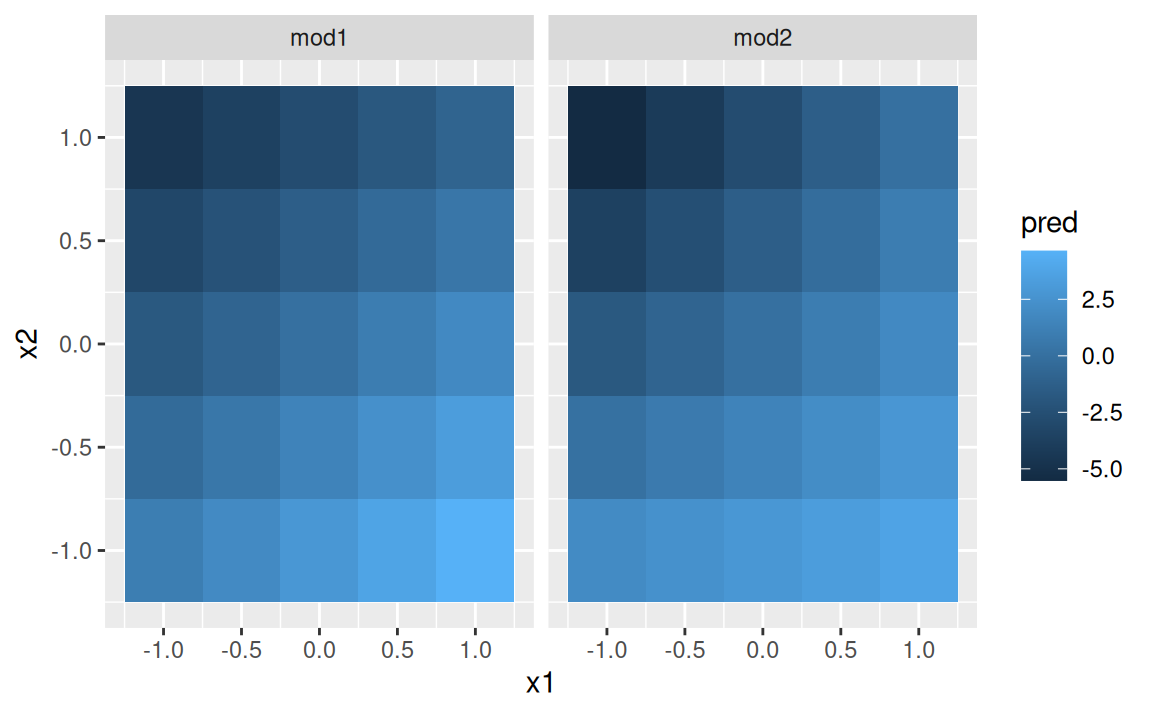
ale ľudský zrak nie je veľmi dobrý v rozlišovaní farebných odtieňov, takže lepšie je zobraziť model zboku:
ggplot(grid) + aes(x2, pred, colour = x1, group = x1) + geom_line() +
viridis::scale_color_viridis(option = "D") +
facet_wrap(~ model)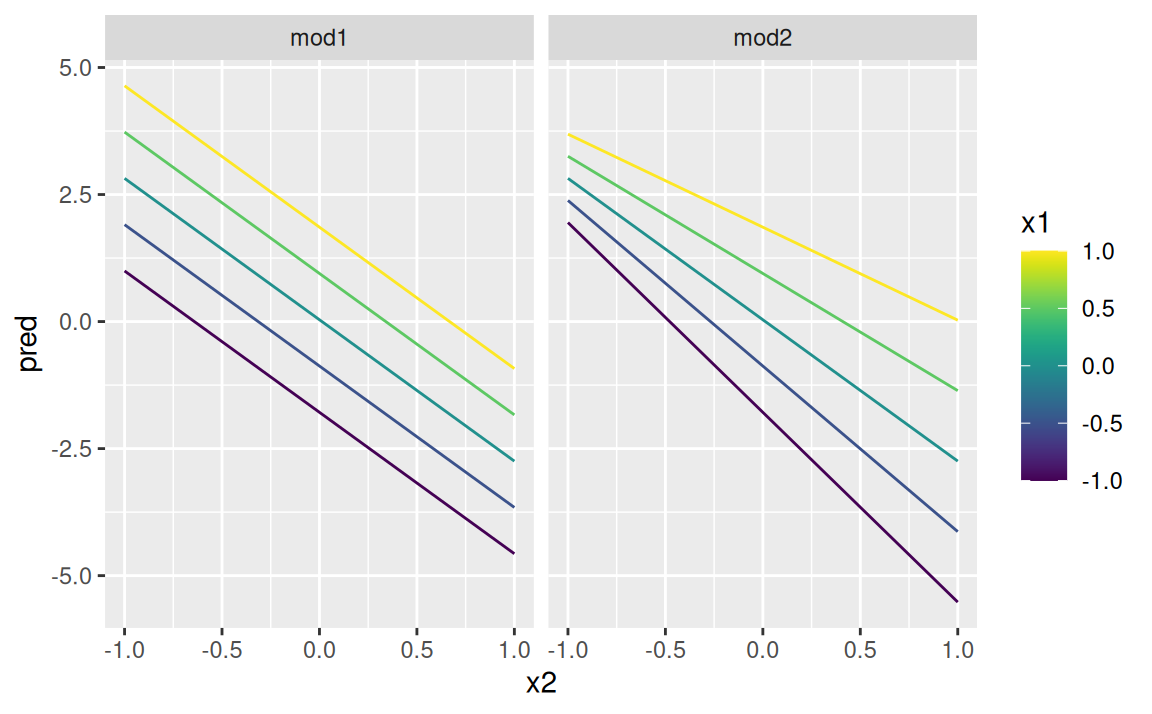
Z oboch príkladov vyplýva to, že s interakciami sa sila závislosti medzi odozvou \(y\) a jedným prediktorom mení v závislosti od hodnoty druhého prediktoru.
7.4.4 Transformácie
Vzťah medzi náhodnými premennými je málokedy lineárny. Videli sme to už pri modeli s interakciou, v ktorom lineárne boli iba rezy v smere jednotlivých premenných. Okrem vynásobenia dvoch premenných sa dá nelinearita vniesť aj transformáciou prediktorov, \(T\), pričom model stále zostáva lineárny v parametroch. V najjednoduchšom prípade má model tvar \[y = b_1 + b_2T(x).\] Bežne používanou transformáciou je
- mocninová, \(T(x) = x^a\),
- exponenciálna \(T(x) = a^x\),
- logaritmická \(T(x) = \log_ax\), či
- trigonometrická \(T(x)=\sin(2\pi x/a)\),
kde \(a\in(0,\infty)\). V lineárnom modeli sú transformácie vlastne bázovými funkciami \(f_i\), takže vo všeobecnosti vieme akýkoľvek lineárny model s \(m\) prediktormi a \(p\) parametrami napísať v tvare \[ y = \sum_{i=1}^p b_if_i(x_1,\ldots,x_m) \] V prípade jednoduchého modelu \(y = b_1 + b_2 x_1\) sa bázové funkcie zredukujú na konštantnú funkciu \(f_1(x)=1\) a identitu \(f_2(x)=x\).
Voľbu bázových funkcií treba zvážiť podľa charakteru signálu identifikovaného počas prieskumnej analýzy. Môže nám to jednak ušetriť niekoľko parametrov v modeli, jednak pomôcť v jeho interpretácii. Počet parametrov súvisí s komplikovanosťou modelu: príliš jednoduchý model celkom nevystihne predpovedateľný vzorec v dátach, a na druhej strane, príliš zložitý model sa snaží popísať už aj šum, ktorý je náhodný, nepredpovedateľný (tento jav sa angl. nazýva overfitting).
V nasledujúcom príklade tri trojparametrické modely súťažia o cenu za najlepší popis umelo vygenerovaných dát. Keďže majú rovnaký počet parametrov, malo by ísť o férový súboj:
sim5 <- tibble::tibble(
x = seq(0, 7 * pi, length = 50),
y = 2 + 4 * sin(2*pi*(x-3)/12) + rnorm(length(x))
)
mod1 <- lm(y ~ x + I(x^2), sim5) # alebo y ~ poly(x, 2)
mod2 <- lm(y ~ sin(2*pi*x/12) + cos(2*pi*x/12), sim5)
mod3 <- lm(y ~ splines::ns(x,2), sim5)
grid <- sim5 |>
modelr::data_grid(x = modelr::seq_range(x, n = 50, expand = 0.1)) |>
modelr::gather_predictions(mod1, mod2, mod3, .pred = "y")
ggplot(sim5) + aes(x, y) + geom_point() +
geom_line(data = grid, aes(colour = model))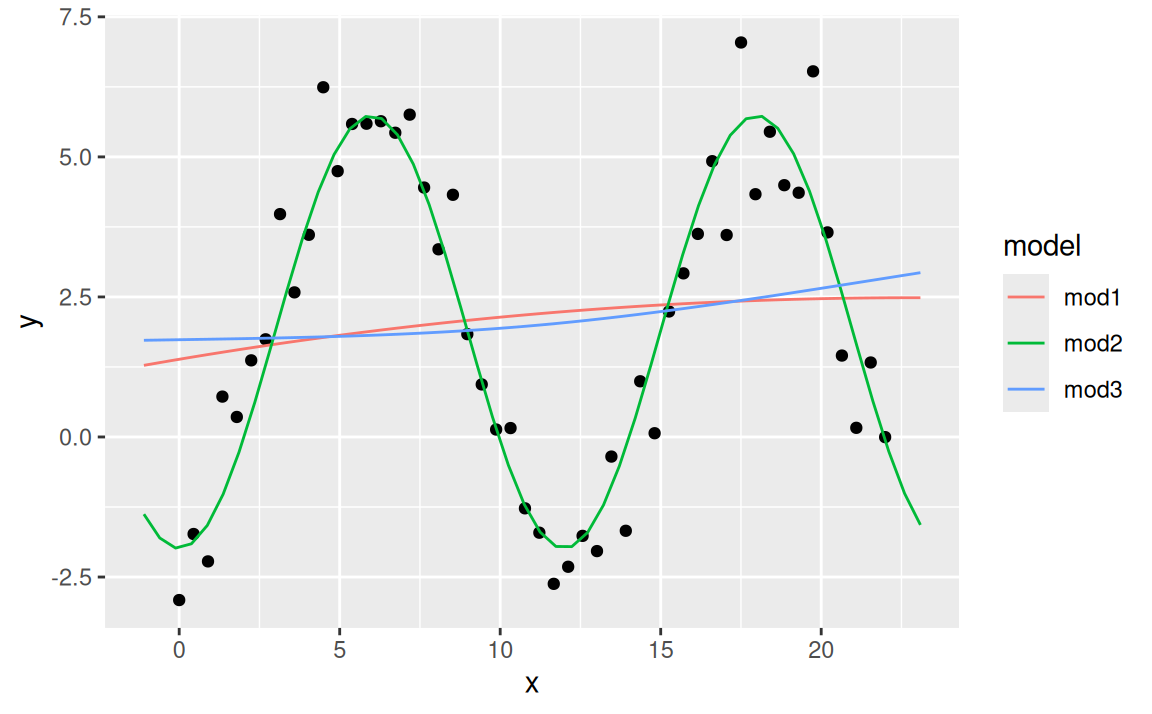
Férový však celkom nie je, pretože v trigonometrickom polynóme sme použili periódu 12 ako známy (hyper)parameter, ktorý by sa inak musel nájsť spektrálnou analýzou. Tento model dobre vystihuje signál v dátach.
Ostatné dva modely sú na pohľad veľmi podobné, líšia sa však vo všeobecnom tvare svojej triedy. Zatiaľčo kvadratický polynóm v modeli mod1 je definovaný v celom rozsahu \(x\), prirodzený splajn v modeli mod3 sa skladá z dvoch kubických polynómov definovaných medzi tzv. uzlami (a priamok na okrajoch). Zvyšovaním stupňa polynomickej funkcie v mod1 a počtu uzlov (resp. stupňov voľnosti) splajnu v mod3 by došlo k zlepšovaniu aproximačnej schopnosti modelov. Napokon, na taký účel sa aj používajú (líšia sa však v schopnosti extrapolácie):
mod4 <- lm(y ~ poly(x,6), sim5)
mod5 <- lm(y ~ splines::ns(x,df=6), sim5)
grid <- data.frame(x = modelr::seq_range(sim5$x, n = 100, expand = 0.15)) |>
modelr::gather_predictions(mod4, mod5, .pred = "y")
ggplot(sim5) + aes(x, y) + geom_point() +
geom_line(data = grid, aes(colour = model))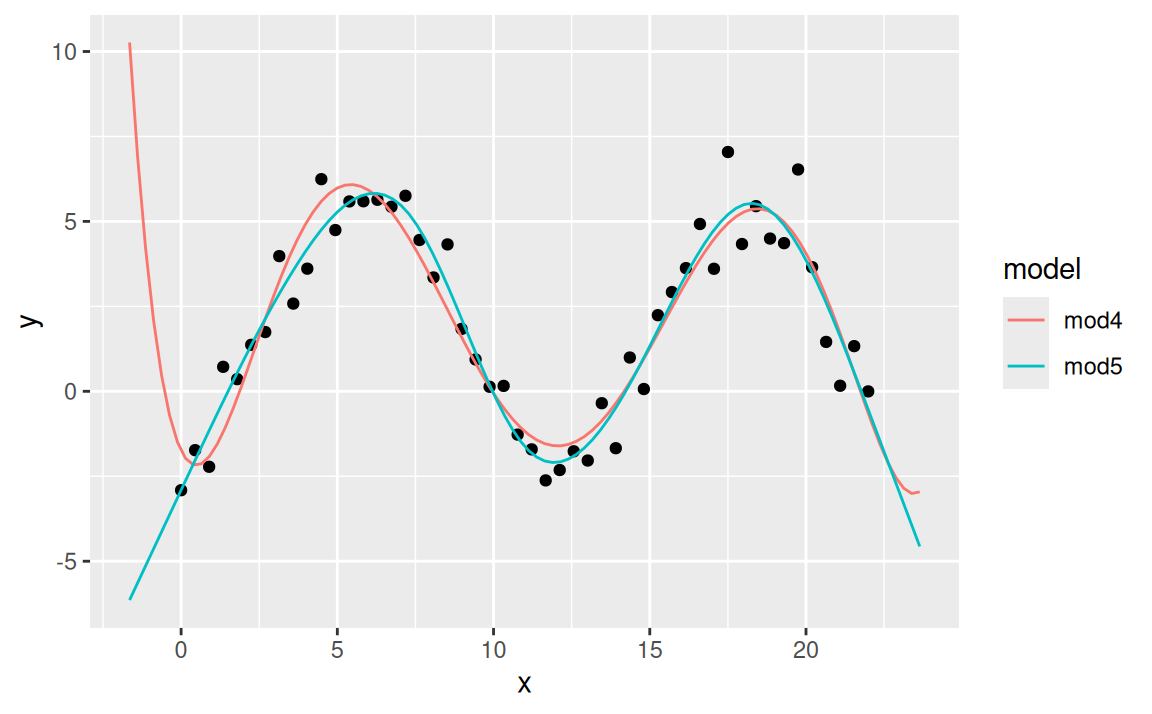 
Keďže vieme, aký mechanizmus (vzorec) generoval dáta sim5, na základe extrapolačných schopností môžme skonštatovať, že oba modely sú nesprávne. Extrapolácia je dôležitá napr. v analýze časových radov.
V praxi sa modely vyhodnocujú na základe toho, ako dobre vystihnú tzv. validačnú vzorku, čiže dáta, na ktorých neboli trénované. Na tomto princípe funguje napr. metóda krížovej validácie modelov (angl. cross-validation).
7.5 Výstavba modelu
V predošlých kapitolách sme si na ilustračných údajoch ukázali odhad modelu, princíp fungovania triedy lineárnych modelov aj použitie základných nástrojov na porozumenie toho, čo model hovorí o dátach. Teraz si na skutočných dátach ukážeme, ako postupná výstavba modelu pomáha v pochopení dát.
Vychádzame zo základnej predstavy, že model štiepi dáta na signál a rezíduá. Najprv pomocou vizualizácie odhalíme nejaký vzorec správania, potom ho pomocou modelu konkretizujeme. Keďže nemusí ísť o jediný vzorec prítomný v dátach, proces opakujeme s rezíduami namiesto pôvodných dát. Nakoniec všetky zložky signálu spojíme v jednom modeli. Takto premieňame implicitnú znalosť dát uloženú v našej hlave na explicitnú znalosť uloženú v kvantitatívnom modeli.
Pre veľké a zložité súbory údajov môže byť tento postup náročný a prácny. Existujú aj alternatívne, jednoduchšie prístupy z oblasti strojového učenia, ktoré sa zameriavajú na predpovednú schopnosť modelu. Presnosťou skutočne excelujú, no zároveň produkujú modely, ktoré sú ako čierne skrinky: nepovedia nám, ako skutočný svet funguje. Ak sa v ňom niečo podstatné zmení, nedokážeme posúdiť, nakoľko spoľahlivé predikcie bude model i naďalej schopný produkovať. To môže byť problém v kritických aplikáciách, kde sú v stávke peniaze či dokonca ľudské životy.3
Tak ako v iných oblastiach života, aj pri výstavbe modelu treba vedieť kedy skončiť. Niekedy je dokonca – namiesto neustáleho vylepšovania – lepšie začať odznova.
7.5.1 Prečo sú menej kvalitné diamanty drahšie?
Dataset ggplot2::diamonds obsahuje cenu a vlastnosti veľkej vzorky brúsených diamantov ako
- hmotnosť (carat),
- kvalitu výbrusu (cut),
- farbu (od najlepšej D po najhoršiu J),
- čírosť (clarity, od najhoršej I1 po najlepšiu IF),
- rozmery (x,y,z) v milimetroch.
Keď sa pozrieme na graf rozdelenia ceny podľa troch vlastností, do očí nám udrie zdanlivý paradox:
library(patchwork)
ytheme <- theme(axis.title.y = element_blank(), # redukcia popisu y osi
axis.text.y = element_blank(), # žiaľ, elegantnejšie to zatiaľ nejde
axis.ticks.y = element_blank())
g <- ggplot(diamonds) + aes(y = price) + geom_boxplot() +
theme(axis.text.x = element_text(angle = 45, hjust=1))
g + aes(x = cut) |
g + aes(x = color) + ytheme |
g + aes(x = clarity) + ytheme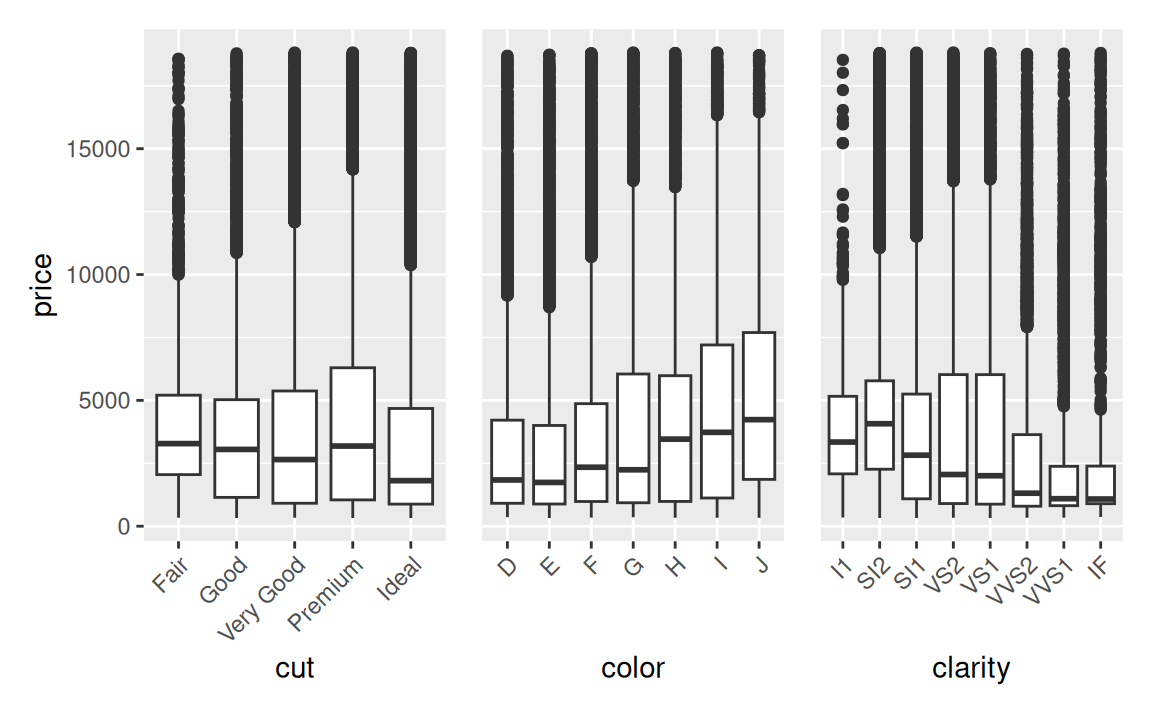
Cena klesá s rastúcou kvalitou (t.j. s výbrusom i čírosťou). Naozaj?!
Tento zjavný nezmysel je však spôsobený vplyvom dôležitého faktora: hmotnosti diamantu. (V literatúre sa zvykne označovať ako mätúca premenná, confounding variable). Hmotnosť diamantu totiž najviac vplýva na cenu, a lacnejšie diamanty bývajú ťažšie.
ggplot(diamonds) + aes(carat, price) +
geom_hex(bins = 50) # k ggplot2 je potrebné doinštalovať balík hexbin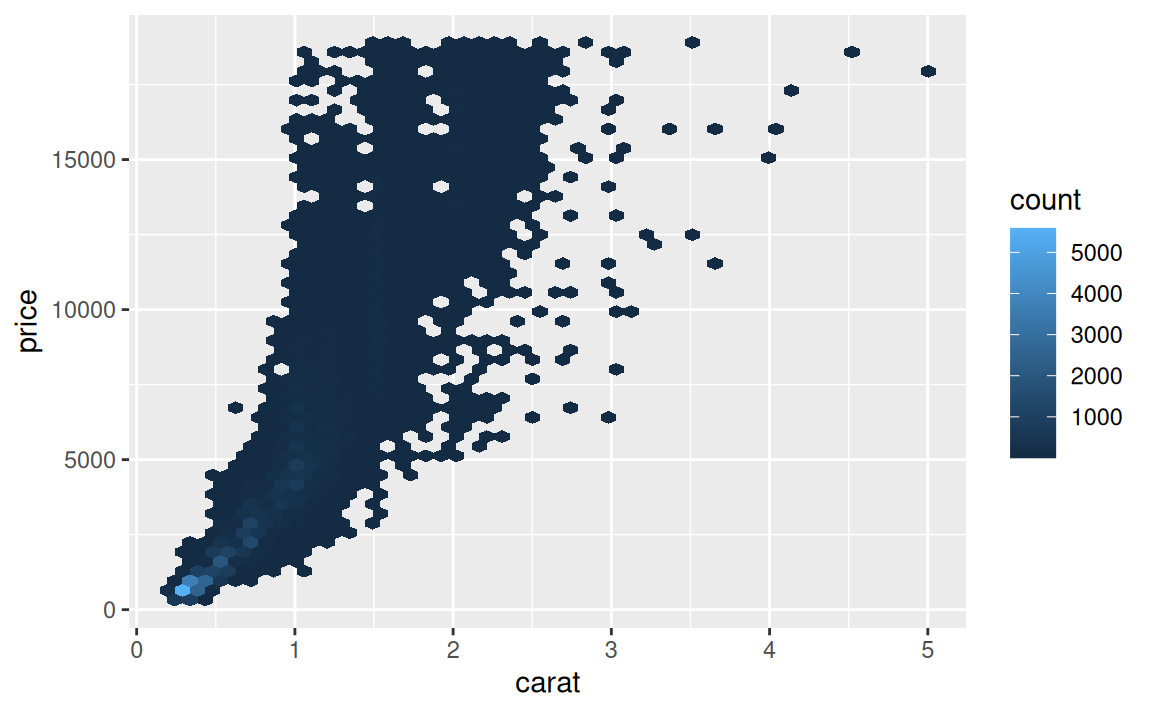
Aby sme ľahšie zbadali, ako ostatné vlastnosti ovplyvňujú cenu, pomocou modelu odfiltrujeme efekt hmotnosti. Ale ešte predtým je dáta výhodné trochu upraviť: odstrániť raritné prípady a transformovať premenné logaritmickou funkciou.
diamonds2 <- diamonds |>
dplyr::filter(carat <= 2.5) |>
dplyr::mutate(lprice = log2(price), lcarat = log2(carat))Odľahlé pozorovania by výrazne skreslili model (pretože pri odhade modelu minimalizujeme štvorce odchýlok) a logaritmická transformácia linearizuje vzťah medzi hmotnosťou a cenou. Taký sa modeluje jednoduchšie.
ggplot(diamonds2) + aes(lcarat, lprice) + geom_hex(bins = 50)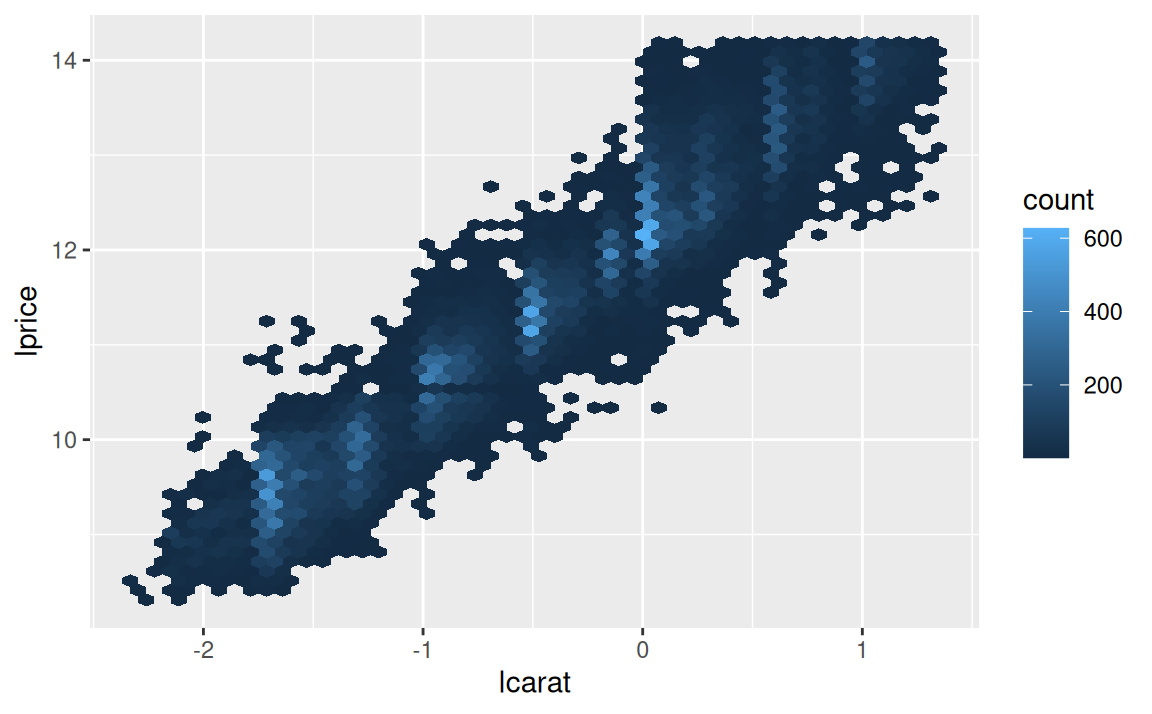
Ďalší krok je explicitné vyjadrenie výrazného vzoru v dátach (pomocou modelu) a jeho odstránenie.
mod1 <- lm(lprice ~ lcarat, data = diamonds2)Pred vykreslením treba predikcie transformovať naspäť do pôvodnej mierky.
grid <- diamonds2 |>
modelr::data_grid(carat = modelr::seq_range(carat, 20)) |>
dplyr::mutate(lcarat = log2(carat)) |>
modelr::add_predictions(mod1, "lprice") |>
dplyr::mutate(price = 2 ^ lprice)
ggplot(diamonds2) + aes(carat, price) +
geom_hex(bins = 50) +
geom_line(data = grid, colour = "red", linewidth = 1)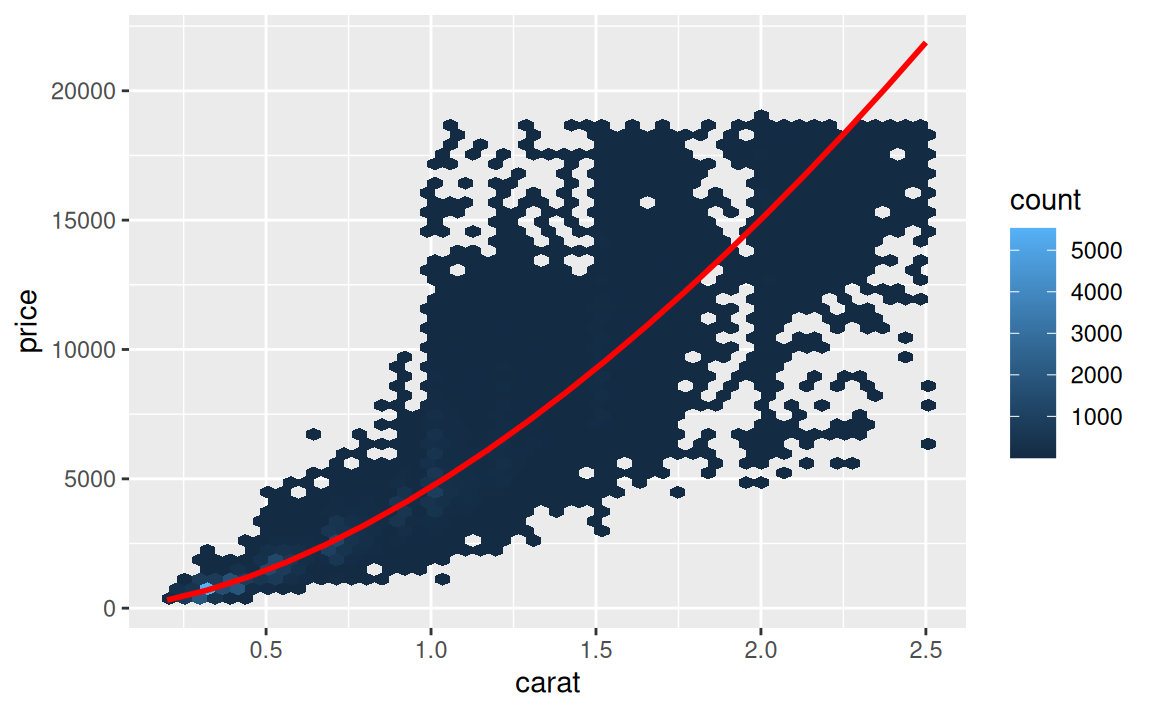
Rezíduá potvrdzujú, že výrazný vzor bol odstránený:
diamonds2 <- diamonds2 |>
modelr::add_residuals(mod1, "lprice_resid")
ggplot(diamonds2) + aes(lcarat, lprice_resid) + geom_hex(bins = 50)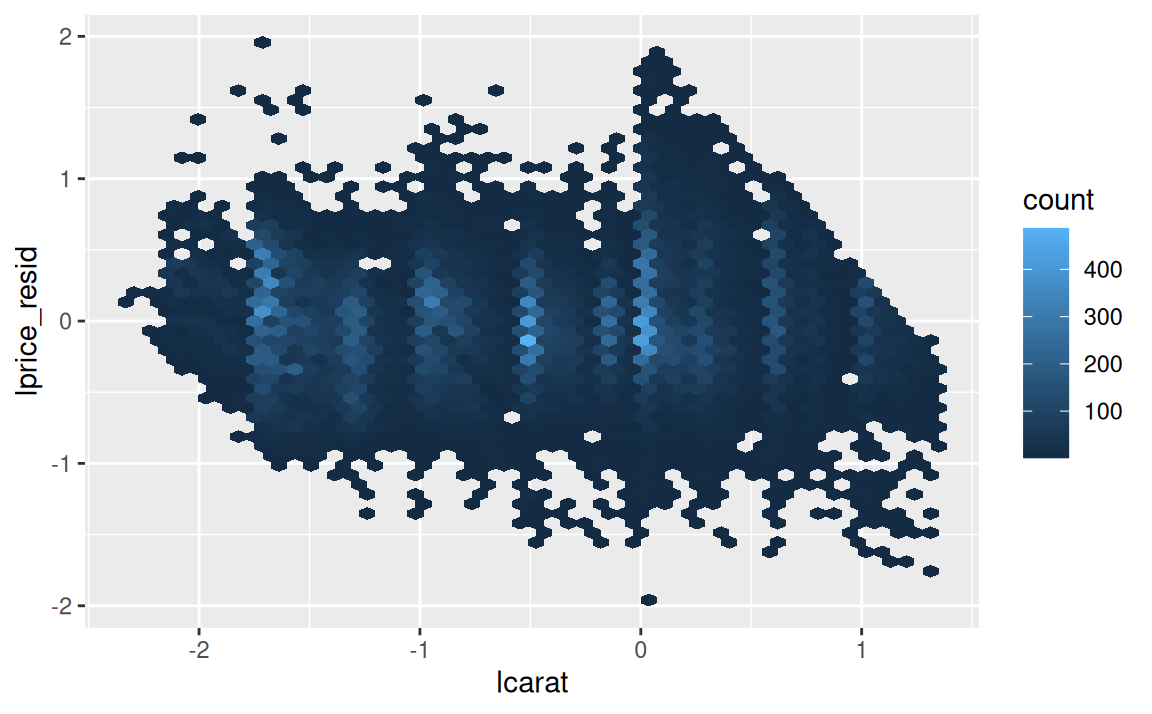
Čo je však dôležitejšie, teraz uvidíme vzťah ceny a vlastností diamantov neskreslený:
g <- ggplot(diamonds2) + aes(y = lprice_resid) + geom_boxplot() +
theme(axis.text.x = element_text(angle = 45, hjust=1))
g + aes(x = cut) |
g + aes(x = color) + ytheme |
g + aes(x = clarity) + ytheme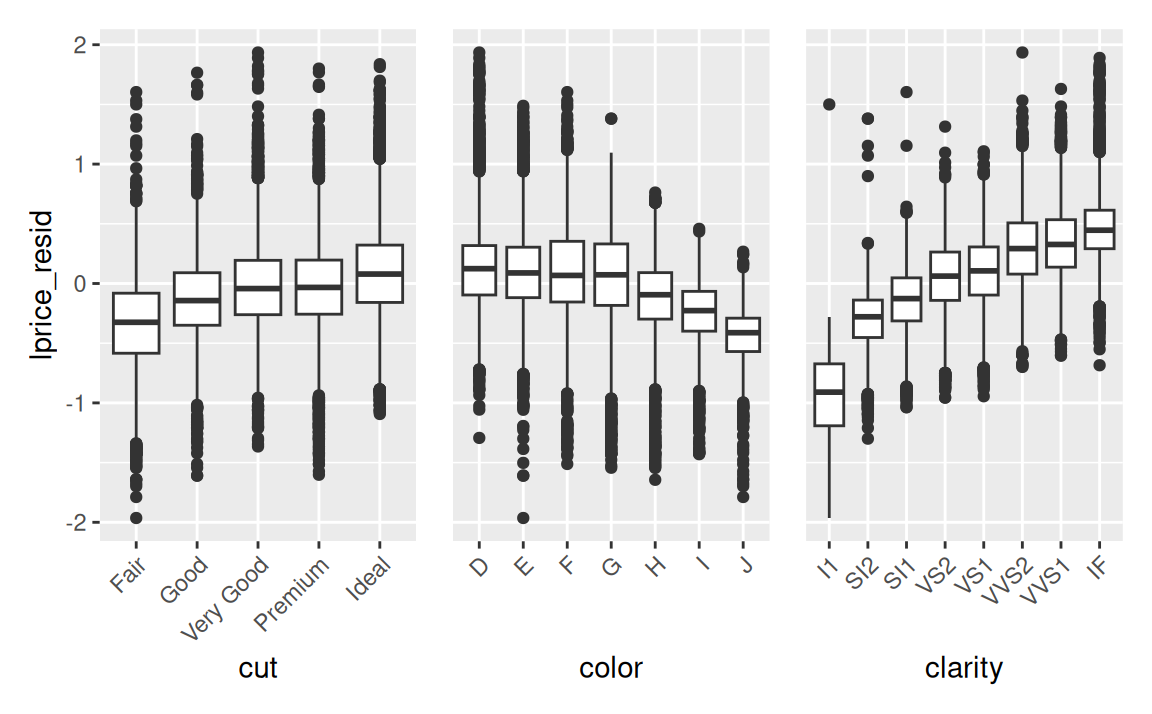
Konečne, cena s kvalitou rastie, tak ako by sme očakávali. Hodnoty na vertikálnej osi však treba správne interpretovať. Rezíduum -1 znamená, že hodnota lprice bola o 1 jednotku nižšia ako predikcia. Pretože sme v logaritmickej mierke so základom 2, a platí \(2^{-1}=1/2\), potom v pôvodnej mierke skutočná cena je polovicou očakávanej ceny (predikcie). Alebo, rezíduum s hodnotou 1 hovorí, že skutočná cena je dvojnásobkom očakávanej.
Keďže sa dá pozorovať vplyv kvality výbrusu, farby a čírosti na cenu diamantu a to aj zodpovedá našej skúsenosti s realitou, môžeme pridať tieto tri kategorické premenné do modelu:
mod2 <- lm(lprice ~ lcarat + color + cut + clarity, data = diamonds2)Model, ktorý obsahuje 4 prediktory je už pomerne náročné zobraziť. Naštastie neobsahuje interakcie, takže sa dá zobraziť po jednotlivých vplyvoch (marginal effects). Napríklad vplyv výbrusu pri „typických” hodnotách ostatných faktorov:
grid <- diamonds2 |>
modelr::data_grid(cut, .model = mod2) |>
modelr::add_predictions(mod2)
grid# A tibble: 5 × 5
cut lcarat color clarity pred
<ord> <dbl> <chr> <chr> <dbl>
1 Fair -0.515 G VS2 11.2
2 Good -0.515 G VS2 11.3
3 Very Good -0.515 G VS2 11.4
4 Premium -0.515 G VS2 11.4
5 Ideal -0.515 G VS2 11.4ggplot(grid) + aes(cut, pred) + geom_point()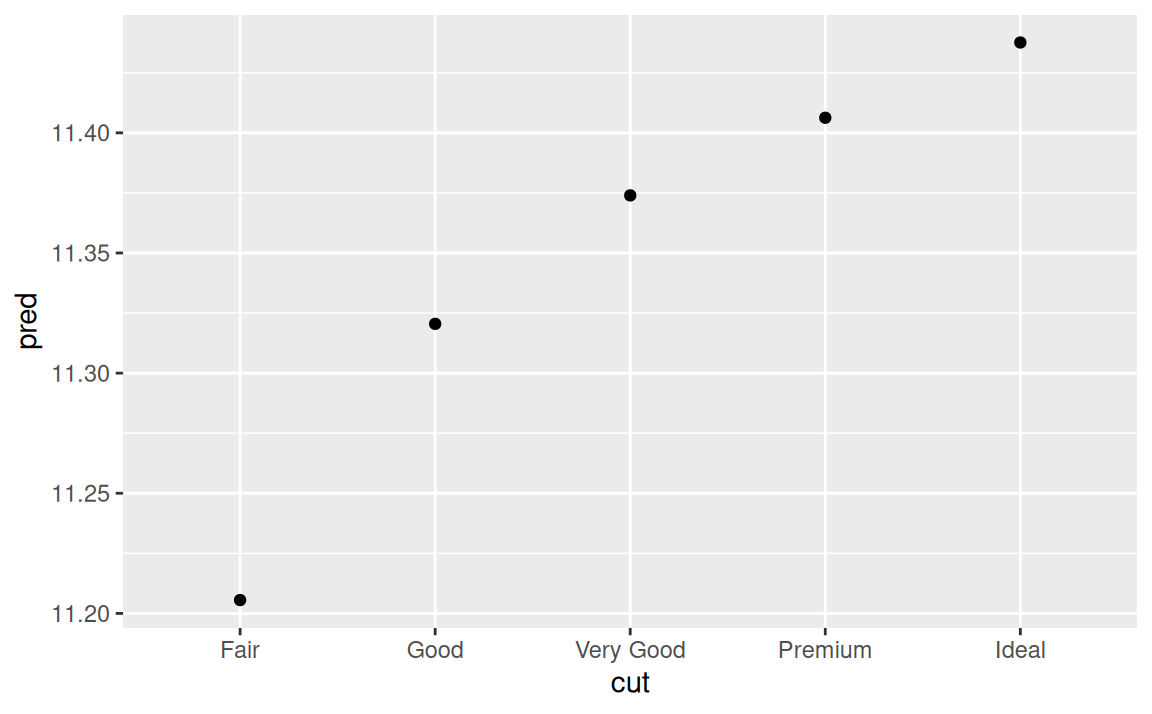
Typickou hodnotou sa myslí modus (najčastejšia hodnota) kategoriálnej premennej a medián v prípade spojitej premennej.
Ešte model zhodnoťme pohľadom na rezíduá:
diamonds2 <- diamonds2 |>
modelr::add_residuals(mod2, "lresid2")
ggplot(diamonds2, aes(lcarat, lresid2)) +
geom_hex(bins = 50)
diamonds2 |>
modelr::add_predictions(mod2, "lpred2") |>
ggplot() + aes(lpred2, lresid2) +
geom_hex(bins = 50)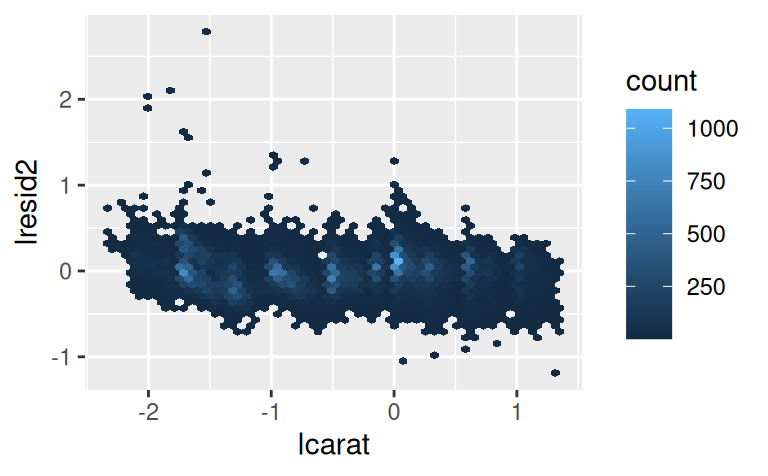
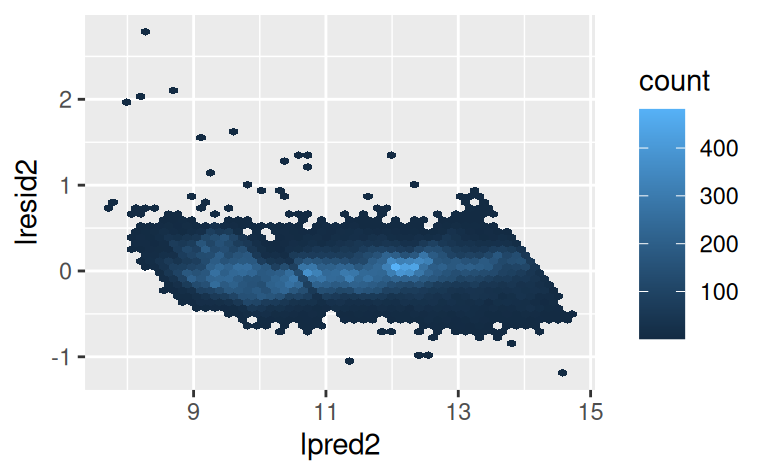
Ceny niektorých diamantov sú veľmi odlišné oproti očakávanej cene (hodnota logaritmu rezídua rovný 2 zodpovedá 4-násobku), inak sú rezíduá rozptýlené okolo nuly celkom normálne. Môže byť užitočné na odľahlé hodnoty pozrieť jednotlivo:
diamonds2 |>
dplyr::filter(abs(lresid2) > 1) |>
modelr::add_predictions(mod2) |>
dplyr::mutate(pred = round(2 ^ pred)) |>
dplyr::arrange(desc(abs(lresid2))) |>
dplyr::select(price, pred, carat:table, x:z)# A tibble: 16 × 11
price pred carat cut color clarity depth table x y z
<int> <dbl> <dbl> <ord> <ord> <ord> <dbl> <dbl> <dbl> <dbl> <dbl>
1 2160 314 0.34 Fair F I1 55.8 62 4.72 4.6 2.6
2 1776 412 0.29 Fair F SI1 55.8 60 4.48 4.41 2.48
3 1186 284 0.25 Premium G SI2 59 60 5.33 5.28 3.12
4 1186 284 0.25 Premium G SI2 58.8 60 5.33 5.28 3.12
5 1013 264 0.25 Fair F SI2 54.4 64 4.3 4.23 2.32
6 2366 774 0.3 Very Good D VVS2 60.6 58 4.33 4.35 2.63
7 1715 576 0.32 Fair F VS2 59.6 60 4.42 4.34 2.61
8 4368 1705 0.51 Fair F VVS2 60.7 66 5.21 5.11 3.13
9 10011 4048 1.01 Fair D SI2 64.6 58 6.25 6.2 4.02
10 3807 1540 0.61 Good F SI2 62.5 65 5.36 5.29 3.33
11 3360 1373 0.51 Premium F SI1 62.7 62 5.09 4.96 3.15
12 3920 1705 0.51 Fair F VVS2 65.4 60 4.98 4.9 3.23
13 10470 23622 2.46 Premium E SI2 59.7 59 8.82 8.76 5.25
14 1415 639 0.35 Fair G VS2 65.9 54 5.57 5.53 3.66
15 1415 639 0.35 Fair G VS2 65.9 54 5.57 5.53 3.66
16 1262 2644 1.03 Fair E I1 78.2 54 5.72 5.59 4.42Jednak pre zistenie príčiny možného zlyhania modelu, jednak pre nájdenie chyby v dátach (alebo investovanie do nedocenených diamantov.)
7.6 Záver
Téma štatistického modelovania je veľmi široká, venujú sa jej konkrétne predmety ako napr. Štatistické metódy v 2. ročníku MPM, Analýza časových radov v 3.MPM, Pokročilé metódy štatistického modelovania v 4.MPM, Hĺbková analýza údajov a strojové učenie v 5.MPM, séria troch predmetov Spracovanie a analýza meraní v odbore GaK na Stavebnej fakulte STU či Štatistické metódy vyhodnocovania experimentov na FIIT STU.
Pre doplnkové alebo samostatné štúdium existuje veľké množstvo literatúry, je náročné odporučiť konkrétne tituly, pretože riešenie konkrétnych problémov v analýze údajov si často vyžaduje individuálny prístup. Z tých všeobecne využiteľných zdrojov na výučbu matematickej štatistiky odporúčame napr.:
- Dalpiaz D.: Applied Statistics with R.
- James, Witten, Hastie, Tibshirani: An Introduction to Statistical Learning.
- Kaplan D.: Statistical Modeling.
- Navarro D.: Learning Statistics with R.
- Shalizi C.: Advanced Data Analysis from an Elementary Point of View.
V Rku sa problematike modelovania z komplexného hľadiska a v duchu filozofie tidyverse venuje súbor balíkov tidymodels.
Kontext citátu:
Now it would be very remarkable if any system existing in the real world could be exactly represented by any simple model. However, cunningly chosen parsimonious models often do provide remarkably useful approximations. For example, the law PV = RT relating pressure P, volume V and temperature T of an “ideal” gas via a constant R is not exactly true for any real gas, but it frequently provides a useful approximation and furthermore its structure is informative since it springs from a physical view of the behavior of gas molecules.
For such a model there is no need to ask the question “Is the model true?”. If “truth” is to be the “whole truth” the answer must be “No”. The only question of interest is “Is the model illuminating and useful?”.↩︎Balík purrr je súbor nástrojov pre funkcionálne programovanie.↩︎
Preto sa v poslednom období hovorí čoraz viac o tzv. vysvetliteľnej umelej inteligencii, angl. explainable artificial intelligence.↩︎